00 写在前面
如何将ipynb文件转为markdown文件?
jupyter nbconvert --to markdown note.ipynb
chapter 01
import numpy as np
# 向量
v = np.array([1,2,3])
# 矩阵
m = np.array([[1,2,3],[4,5,6],[7,8,9]])
# 张量
t = np.array([
[[1,2,3],[4,5,6],[7,8,9]],
[[11,12,13],[14,15,16],[17,18,19]],
[[21,22,23],[24,25,26],[27,28,29]],
])
print("向量:"+str(v))
print("矩阵:"+str(m))
print("张量:"+str(t))
向量:[1 2 3]
矩阵:[[1 2 3]
[4 5 6]
[7 8 9]]
张量:[[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]]
[[11 12 13]
[14 15 16]
[17 18 19]]
[[21 22 23]
[24 25 26]
[27 28 29]]]
1.2 矩阵转置
a = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
a_t = a.transpose()
print(a)
# print one line to separate the two outputs
print('-'*30)
print(a_t)
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
------------------------------
[[ 1 4 7 10]
[ 2 5 8 11]
[ 3 6 9 12]]
1.3 矩阵加法
有时候允许矩阵和向量相加,得到一个矩阵,本质上是构造了一个将b按行复制的一个新矩阵,这种操作叫做广播(broadcasting)。
1.4 矩阵乘法
矩阵乘法的结果是一个矩阵,其第i行第j列的元素是矩阵A的第i行与矩阵B的第j列的内积。A的形状为m×n,B的形状为n×p,那么A×B的形状为m×p。矩阵乘法的计算可以用下面的公式表示: \(c[i,j] = a[i,:] * b[:,j]\)
m1 = np.array([[1.0,3.0],[1.0,0.0]])
m2 = np.array([[1.0,2.0],[3.0,5.0]])
print(m1)
print(m2)
# 矩阵乘法
m3 = np.dot(m1,m2)
print(m3)
# 矩阵按元素相乘
m4 = np.multiply(m1,m2)
# 矩阵按元素相乘
m5 = m1*m2
print(m4)
print(m5)
[[1. 3.]
[1. 0.]]
[[1. 2.]
[3. 5.]]
[[10. 17.]
[ 1. 2.]]
[[1. 6.]
[3. 0.]]
[[1. 6.]
[3. 0.]]
1.5 单位矩阵
单位矩阵是一个方阵,对角线上的元素为1,其余元素为0。单位矩阵的作用是不改变矩阵的值,它乘以任何矩阵都等于原矩阵。
np.identity(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
1.6 矩阵的逆
矩阵A的逆(inverse)是一个矩阵B,使得A×B=I,其中I是单位矩阵。矩阵A的逆记为$A^{−1}$。如果A是一个方阵,那么A的逆也是一个方阵。如果A的逆存在,那么A的逆也叫做A的伪逆(pseudo-inverse)。
A = [[1,2],[4,5]]
A_inv = np.linalg.inv(A)
print(A_inv)
[[-1.66666667 0.66666667]
[ 1.33333333 -0.33333333]]
1.7范数 norm
向量$L^P$范数定义为:
\(||x||_p = (\sum_{i=1}^n |x_i|^p)^{1/p},p\geq 1,p\in\mathbb{R}\)
L1范数:向量中各个元素绝对值之和
\(||x||_1 = \sum_{i=1}^n |x_i|\)
L0范数:向量中非零元素的个数
\(||x||_0 = \sum_{i=1}^n \mathbb{1}(x_i\neq 0)\)
L2范数:向量中各个元素平方和的平方根,也叫欧式范数,是向量x到原点的欧几里得距离,有时候也用L2范数的来衡量向量:$x^Tx$.
\(||x||_2 = \sqrt{\sum_{i=1}^n x_i^2}\)
L∞范数:向量中各个元素绝对值的最大值
\(||x||_\infty = \max_{i=1,\cdots,n}|x_i|\)
机器学习中常用的范数有L1范数和L2范数,L1范数用于稀疏性的优化,L2范数用于凸优化。
import numpy as np
a = np.array([1.0,3.0,5.0])
print("向量的2范数:"+str(np.linalg.norm(a,ord=2)))
print("向量的1范数:"+str(np.linalg.norm(a,ord=1)))
print("向量的无穷范数:"+str(np.linalg.norm(a,ord=np.inf)))
# 矩阵才有Frobenius范数
b = np.array([[1.0,3.0,5.0],[2.0,4.0,6.0]])
print('向量的Frobenius范数:'+str(np.linalg.norm(b,ord='fro')))
向量的2范数:5.916079783099616
向量的1范数:9.0
向量的无穷范数:5.0
向量的Frobenius范数:9.539392014169456
1.8 特征值分解
如果一个n×n的矩阵A有n组线性无关的单位特征向量{$v^1$, $v^2$, $\cdots$, $v^n$},并且对应的特征值为{$\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_n$},那么矩阵A可以被分解为:
\(A = V diag(\lambda) V^{-1}\)
不是所有的矩阵都有特征值分解,如果A是一个n×n的矩阵,那么A的特征值分解存在当且仅当A是可逆的且A的行列式不为0。如果A的特征值分解存在,那么A的特征值分解是唯一的。
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
# 计算特征值
eig_value,eig_vector = np.linalg.eig(A)
print("特征值:"+str(eig_value))
print("特征向量:"+str(eig_vector))
特征值:[ 1.61168440e+01 -1.11684397e+00 -1.30367773e-15]
特征向量:[[-0.23197069 -0.78583024 0.40824829]
[-0.52532209 -0.08675134 -0.81649658]
[-0.8186735 0.61232756 0.40824829]]
1.9 奇异值分解
奇异值分解(Singular Value Decomposition,SVD)是一种矩阵分解方法,它将一个矩阵分解为奇异向量和奇异值,它的分解形式如下:
\(A = U\Sigma V^T\)
若A是m×n的矩阵,那么U是m×m的正交矩阵(其列向量称为左奇异向量),V是n×n的正交矩阵(其列向量称为右奇异向量),$\Sigma$是m×n的对角矩阵(对角线上的元素称为奇异值)。奇异值分解的作用是将一个矩阵分解为三个矩阵的乘积,这三个矩阵分别是正交矩阵和对角矩阵,这样就可以将矩阵的秩降低,从而达到降维的目的。
事实上,左奇异向量式$AA^T$的特征向量,右奇异向量是$A^TA$的特征向量,奇异值是$AA^T$特征值的平方根。
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
U,D,V= np.linalg.svd(A)
print("U:"+str(U))
print("D:"+str(D))
print("V:"+str(V))
U:[[-0.21483724 0.88723069 0.40824829]
[-0.52058739 0.24964395 -0.81649658]
[-0.82633754 -0.38794278 0.40824829]]
D:[1.68481034e+01 1.06836951e+00 4.41842475e-16]
V:[[-0.47967118 -0.57236779 -0.66506441]
[-0.77669099 -0.07568647 0.62531805]
[-0.40824829 0.81649658 -0.40824829]]
1.10 PCA分解
假设我们有m个数据点$x^1,x^2,\cdot,x^m \in \mathbb{R}^n$,每个数据点是一个n维的向量,我们希望将这些数据点投影到一个l维的空间中(降纬之后的损失信息尽可能地少),使得投影后的数据点之间的距离尽可能的大,而投影后的数据点与原始数据点之间的距离尽可能的小。这就是PCA分解。
PCA分解是线性变化,假设$x^i$分解之后的对应点为$c^i$,那么有:
\(f(x) =c\)
\(c \approx =g(f(x))\)
\(g(c)=Dc,D \in \mathbb{R}^{n\times l}\)
为了计算方便,我们将这个矩阵的列向量约束为相互正交的;而且,考虑到尺度缩放的问题,我们将这个矩阵的列向量约束为具有单位范数来获得唯⼀解。
对于给定的x,我们需要找到信息损失最小的$\boldsymbol{c}^{\star}$:
\(\boldsymbol{c}^{\star}=\arg \min _{\boldsymbol{c}}\|\boldsymbol{x}-g(\boldsymbol{c})\|_2=\arg \min _{\boldsymbol{c}}\|\boldsymbol{x}-g(\boldsymbol{c})\|_2^2\)
这里我们用二范数来衡量信息的损失。展开之后我们有:
\(\|\boldsymbol{x}-g(\boldsymbol{c})\|_2^2=(\boldsymbol{x}-g(\boldsymbol{c}))^{\top}(\boldsymbol{x}-g(\boldsymbol{c}))=\boldsymbol{x}^{\top} \boldsymbol{x}-2 \boldsymbol{x}^{\top} g(\boldsymbol{c})+g(\boldsymbol{c})^{\top} g(\boldsymbol{c})\)
结合 $g(\boldsymbol{c})$ 的表达式, 忽略不依赖 $\boldsymbol{c}$ 的 $\boldsymbol{x}^{\top} \boldsymbol{x}$ 项, 我们有:
\(\begin{aligned}
\boldsymbol{c}^{\star} & =\arg \min _{\boldsymbol{c}}-2 \boldsymbol{x}^{\top} \boldsymbol{D} \boldsymbol{c}+\boldsymbol{c}^{\top} \boldsymbol{D}^{\top} \boldsymbol{D} \boldsymbol{c} \\
& =\arg \min _{\boldsymbol{c}}-2 \boldsymbol{x}^{\top} \boldsymbol{D} \boldsymbol{c}+\boldsymbol{c}^{\top} \boldsymbol{I}_l \boldsymbol{c} \\
& =\arg \min _{\boldsymbol{c}}-2 \boldsymbol{x}^{\top} \boldsymbol{D} \boldsymbol{c}+\boldsymbol{c}^{\top} \boldsymbol{c}
\end{aligned}\)
这里 $\boldsymbol{D}$ 具有单位正交性。
对 $\boldsymbol{c}$ 求梯度, 并令其为零, 我们有:
因此, 我们的编码函数为:
\(f(x)=D^{\top} \boldsymbol{x}\)
此时通过编码解码得到的 $重构\boldsymbol{x}$ 为:
\(r(x)=g(f(x))=DD^{\top}x\)
接下来求解最优的变换 $\boldsymbol{D}$ 。由于我们需要将 $\boldsymbol{D}$ 应用到所有的 $\boldsymbol{x}_i$ 上,所以我们需要最优化:
\(\begin{array}{l}
\boldsymbol{D}^{\star}=\arg \min _{\boldsymbol{D}} \sqrt{\sum_{i, j}\left(\boldsymbol{x}_j^{(i)}-r\left(\boldsymbol{x}^{(i)}\right)_j\right)^2} \\
\text { s.t. } \boldsymbol{D}^{\top} \boldsymbol{D}=\boldsymbol{I}_l
\end{array}\)
为了方便, 我们考虑 $l=1$ 的情况, 此时问题简化为:
\(\begin{array}{l}
\left.\boldsymbol{d}^{\star}=\arg \min _{\boldsymbol{d}} \sum_i\left(\boldsymbol{x}_j^{(i)}-\boldsymbol{d} \boldsymbol{d}^{\top} \boldsymbol{x}^{(i)}\right)\right)^2 \\
\text { s.t. } \boldsymbol{d}^{\top} \boldsymbol{d}=1
\end{array}\)
考虑 $\mathrm{F}$ 范数, 并进一步的推导:
\(\begin{array}{l}
\boldsymbol{d}^{\star}=\arg \max _{\boldsymbol{d}} \operatorname{Tr}\left(\boldsymbol{d}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{d}\right) \\
\text { s.t. } \boldsymbol{d}^{\top} \boldsymbol{d}=1
\end{array}\)
优化问题可以用特征值分解来求解。
实际计算中,PCA分解的实现是基于SVD分解的,即假设有一个 $m \times n$ 的矩阵 $\boldsymbol{X}$, 数据的均值为零, 即 $\mathbb{E}[\boldsymbol{x}]=0, \boldsymbol{X}$ 对应的无偏样本协方差矩阵: $\operatorname{Var}[\boldsymbol{x}]=\frac{1}{m-1} \boldsymbol{X}^{\top} \boldsymbol{X}^{\mathrm{d}}$
PCA 是通过线性变换找到一个 $\operatorname{Var}[c]$ 是对角矩阵的表示 $\boldsymbol{c}=\boldsymbol{V}^{\top} \boldsymbol{x}$, 矩阵 $\boldsymbol{X}$ 的主成分可以通过奇异值分解 (SVD) 得到, 也就是说主成分是 $\boldsymbol{X}$ 的右奇异向量。假设 $\boldsymbol{V}$ 是 $\boldsymbol{X}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}$ 奇异值分解的右奇异向量, 我们得到原来的特征向量方程: \(\boldsymbol{X}^{\top} \boldsymbol{X}=\left(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\right)^{\top} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}=\boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}=\boldsymbol{V} \boldsymbol{\Sigma}^2 \boldsymbol{V}^{\top}\) 因为根据奇异值的定义 $\boldsymbol{U}^{\top} \boldsymbol{U}=\boldsymbol{I}$ 。因此 $\boldsymbol{X}$ 的方差可以表示为: $\operatorname{Var}[\boldsymbol{x}]=\frac{1}{m-1} \boldsymbol{X}^{\top} \boldsymbol{X}=\frac{1}{m-1} \boldsymbol{V} \boldsymbol{\Sigma}^2 \boldsymbol{V}^{\top}$ 。 所以 $\boldsymbol{c}$ 的协方差满足: $\operatorname{Var}[\boldsymbol{c}]=\frac{1}{m-1} \boldsymbol{C}^{\top} \boldsymbol{C}=\frac{1}{m-1} \boldsymbol{V}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{V}=\frac{1}{m-1} \boldsymbol{V}^{\top} \boldsymbol{V} \boldsymbol{\Sigma}^2 \boldsymbol{V}^{\top} \boldsymbol{V}=\frac{1}{m-1} \boldsymbol{\Sigma}^2$, 因为根据奇异值定义 $\boldsymbol{V}^{\top} \boldsymbol{V}=\boldsymbol{I}$ 。 $\boldsymbol{c}$ 的协方差是对 角的, $c$ 中的元素是彼此无关的。
# 以 iris 数据为例,展⽰ PCA 的使⽤。
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
%matplotlib inline
# 载入数据
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
# 查看数据
df.tail()
| sepal length | sepal width | petal length | petal width | label | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
# 准备数据
X = df.iloc[:,0:4]# 取前4列为特征
y =df.iloc[:,4]# 最后一列为标签
class PCA():
def __init(self):
pass
def fit(self,X,n_components):
n_samples = np.shape(X)[0]
covariance_matrix = 1/(n_samples-1) * (X-X.mean(axis=0)).T.dot(X-X.mean(axis=0))
# 对协方差矩阵进行特征值分解
eig_vals, eig_vecs = np.linalg.eig(covariance_matrix)
# 对特征值进行降序排序
idx = eig_vals.argsort()[::-1]
eig_vals = eig_vals[idx][:n_components] # 取前n个特征值
# atleast_1d函数将输入转换为至少为1维的数组
eig_vecs = np.atleast_1d(eig_vecs[:,idx])[:,:n_components]
# 得到降纬之后的数据
X_transformed = X.dot(eig_vecs)
return X_transformed
model = PCA()
Y = model.fit(X,2)# 降维到2维
# 降维后的数据,2列,分别是pca1和pca2,columns表示列名
pcaDf = pd.DataFrame(np.array(Y),columns=['pca1','pca2'])
Df = pd.concat([pcaDf,y],axis=1)# axis =1表示列合并
ax= plt.figure(figsize = (5,5))
ax = plt.subplot(1,1,1)
ax.set_xlabel('pca1',fontsize = 15)
ax.set_ylabel('pca2',fontsize = 15)
targets = [0,1,2] # 3个类别
colors = ['r','g','b'] # 3种颜色,表示3个类别
# for target,color in zip(targets,colors):
# ax.scatter(Df[Df['label']==target]['pca1'],Df[Df['label']==target]['pca2'],c=color,s=50)
for target,color in zip(targets,colors):
indicesToKeep = Df['label'] == target
ax.scatter(Df.loc[indicesToKeep,'pca1'],Df.loc[indicesToKeep,'pca2'],c=color,s =50)
ax.legend(targets)
# title
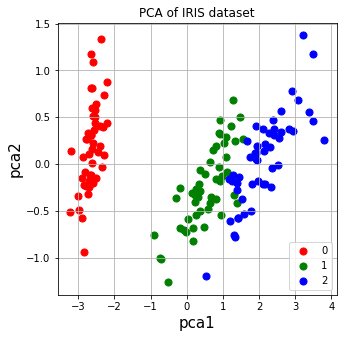
ax.set_title('PCA of IRIS dataset')
ax.grid()
# 使用sklearn实习PCA
from sklearn.decomposition import PCA
sklearn_pca = PCA(n_components=2)
Y = sklearn_pca.fit_transform(X)
PCADf = pd.DataFrame(np.array(Y),columns=['pca1','pca2'])
Df = pd.concat([PCADf,y],axis=1)
ax= plt.figure(figsize = (5,5))
ax = plt.subplot(1,1,1)
ax.set_xlabel('pca1',fontsize = 15)
ax.set_ylabel('pca2',fontsize = 15)
targets = [0,1,2] # 3个类别
colors = ['r','g','b'] # 3种颜色,表示3个类别
for target,color in zip(targets,colors):
indicesToKeep = Df['label'] == target
ax.scatter(Df.loc[indicesToKeep,'pca1'],Df.loc[indicesToKeep,'pca2'],c=color,s =50)
ax.legend(targets)
# title
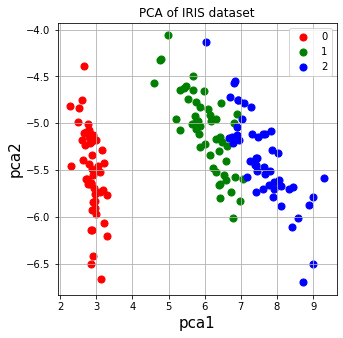
ax.set_title('PCA of IRIS dataset')
ax.grid()