02 概率论与信息论
2.1.1 概论与随机变量
频率学派概率(frequency probability):概率和事件发生的频率相关。频率是指事件发生的次数与事件总次数的比值。频率学派概率的缺点是,它只能用于离散事件,而不能用于连续事件。因为连续事件的发生次数是无穷的,而事件总次数是有限的,所以它们的比值是无穷小的,这样就无法用频率来表示概率了。因此,频率学派概率只能用于离散事件,而不能用于连续事件。 贝叶斯学派概率(bayesian probability):概率和事件发生的先验知识相关。也就是说,概率是对某件事情发生的信心程度的度量。每次事件发生,都会更新先验知识,从而得到后验知识。贝叶斯学派概率的缺点是,它需要先验知识,而先验知识往往是不确定的,所以贝叶斯学派概率也是不确定的。 随机变量(random variable)变量:一个可能随机取不同值的变量,如,抛硬币的结果,掷骰子的结果,抽取的样本的特征等。随机变量的取值是随机的,但是随机变量的取值是有限的,所以随机变量是离散的。
2.1.2 随机变量的分布
概论质量函数(probability Mass Function),对于离散型变量,我们先定义一个随机变量,然后用概率质量函数来描述这个随机变量的取值分布。概率质量函数是一个函数,它的输入是随机变量的取值,输出是随机变量取这个值的概率。概率质量函数的定义是,对于离散型随机变量X,它的概率质量函数是一个函数P(x),它的定义域是随机变量X的取值集合。
如一个离散型x有k个不同的取值,假设x是均匀分布的,那么概率质量函数为:
\(P(x=x^i)=\frac{1}{k}\)
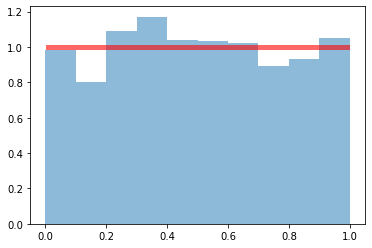
概论密度函数(probability Density Function),对于连续型变量,我们先定义一个随机变量,然后用概率密度函数来描述这个随机变量的取值分布。概率密度函数是一个函数,它的输入是随机变量的取值,输出是随机变量取这个值的概率。概率密度函数的定义是,对于连续型随机变量X,它的概率密度函数是一个函数P(x),它的定义域是随机变量X的取值集合。P(x)是一个非负的函数,它的积分是1,即:
\(\int_{-\infty}^{\infty}P(x)dx=1\)
且满足非负性:
\(\forall x \in \mathbb{X}, P(x)\geq 0\)
累计分布函数(cumulative distribution function)表示对小于x的概率进行积分,即:
\(CDF(x)=\int_{-\infty}^{x}P(x)dx\)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
%matplotlib inline
# generate the sample
fig,ax = plt.subplots(1,1)
# 使用参数loc和scale,可以得到[loc, loc + scale]上的均匀分布,size=1000表示样本数,random_state=123表示随机种子
r = uniform.rvs(loc=0,scale=1,size=1000,random_state=123)
# density=True表示概率密度,histtype='stepfilled'表示填充,alpha=0.5表示透明度
ax.hist(r,density=True,histtype='stepfilled',alpha=0.5)
# 均匀分布pdf
x = np.linspace(uniform.ppf(0.01),uniform.ppf(0.99),100)
ax.plot(x,uniform.pdf(x),'r-',lw=5,alpha =0.6,label='uniform pdf')
[<matplotlib.lines.Line2D at 0x277a8b4d400>]
2.1.3 条件概论与条件独立
边缘概论(Marginal Probability)如果我们知道了一组变量的联合概论分布,想要了解其中一个子集的概率分布。这种定义在子集上的概率分布成为边缘概论分布:
\(\forall x \in \mathbb{X},P(\mathrm{x}=x) = \sum_y P(\mathrm{x}=x,\mathrm{y}=y)\)
条件概论(conditional probability)在很多情况下,我们不仅关心一个事件的概率,还关心在另一个事件发生的条件下,这个事件的概率。这种在另一个事件发生的条件下,事件的概率称为条件概论。条件概论的定义是:
\(P(\mathrm{x}=x|\mathrm{y}=y)=\frac{P(\mathrm{x}=x,\mathrm{y}=y)}{P(\mathrm{y}=y)}\)
这个公式表示在y发生的条件下,x发生的概率。
条件概论的链式法则(chain rule of conditional probability):任何多维随机变量的联合概论分布,都可以分解成只有只有一个变量的条件概论相乘的形式
\(P(\mathrm{x}=x,\mathrm{y}=y,\mathrm{z}=z)=P(\mathrm{x}=x|\mathrm{y}=y,\mathrm{z}=z)P(\mathrm{y}=y,\mathrm{z}=z)=P(\mathrm{x}=x|\mathrm{y}=y,\mathrm{z}=z)P(\mathrm{y}=y|\mathrm{z}=z)P(\mathrm{z}=z)\)
独立性(independence)如果两个随机变量X和Y满足:
\(P(\mathrm{x}=x,\mathrm{y}=y)=P(\mathrm{x}=x)P(\mathrm{y}=y)\)
也即是联合概论分布可以表示成只有一个变量的条件概论相乘的形式。
条件独立性(conditional independence)如果关于x和y的条件概率分布对于z的每一个值都满足独立性,那么我们就说x和y在z的条件下是条件独立的。
\(P(\mathrm{x}=x,\mathrm{y}=y|\mathrm{z}=z)=P(\mathrm{x}=x|\mathrm{z}=z)P(\mathrm{y}=y|\mathrm{z}=z)\)
2.1.4 随机变量的度量
期望(expectation)是随机变量的平均值,期望的定义是:
\(E(X)=\sum_x xP(X=x)\)
对于连续型随机变量可以通过积分的形式表示:
\(E(X)=\int_{-\infty}^{\infty}xP(X=x)dx\)
另外,期望是线性的,即:
\(E(aX+bY)=aE(X)+bE(Y)\)
方差(variance)是随机变量的离散程度,方差的定义是:
\(Var(X)=E[(X-E(X))^2]\)
标准差(standard deviation)是方差的平方根,标准差的定义是:
\(\sigma(X)=\sqrt{Var(X)}\)
协方差(covariance)是两个随机变量的线性相关程度,协方差的定义是:
\(Cov(X,Y)=E[(X-E(X))(Y-E(Y))]\)
注意协方差的符号表示两个随机变量的线性相关程度,正数表示正相关,负数表示负相关,0表示不相关。
注意独立与零协方差更强,因为独立还排除了非线性的相关。
x= np.array([1,2,3,4,5,6,7,8,9,10])
y = np.array([10,9,8,7,6,5,4,3,2,1])
Mean = np.mean(x)
Var = np.var(x)
Var_unbiased = np.var(x,ddof=1)# ddof=1表示无偏估计
Std = np.std(x)
Cov = np.cov(x,y)
Mean,Var,Var_unbiased,Std,Cov
(5.5,
8.25,
9.166666666666666,
2.8722813232690143,
array([[ 9.16666667, -9.16666667],
[-9.16666667, 9.16666667]]))
2.1.5 常用概率分布
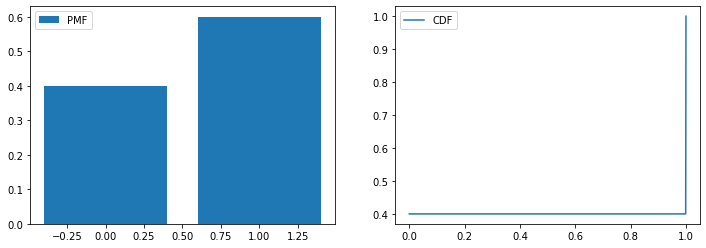
伯努利分布(Bernoulli distribution)是一个二项分布的特例,它只有两个可能的取值,0和1,它的概率质量函数是(表示一次实验成功的概率):
\(P(X=1)=p\),
\(P(X=0)=1-p\),
\(P(X=x)=p^x(1-p)^{1-x}\)
def plot_distribution(X,axes=None):
'''给定随机变量X,绘制其PDF,PMF,CDF'''
if axes is None:
fig,axes = plt.subplots(1,3,figsize=(12,4))
x_min,x_max = X.interval(0.99)# 99%的概率密度在区间内
x = np.linspace(x_min,x_max,1000)
# 连续型变量,画PDF;离散型变量,画PMF
if hasattr(X.dist,'pdf'):
# axes[0]表示第一行,第一列
axes[0].plot(x,X.pdf(x),label='PDF')
axes[0].fill_between(x,X.pdf(x),alpha=0.5) # 填充,透明度0.5
else:
x_int = np.unique(x.astype(int))# 取整,unique去重
axes[0].bar(x_int,X.pmf(x_int),label='PMF')
# CDF
axes[1].plot(x,X.cdf(x),label='CDF')
for ax in axes:
ax.legend()
return axes
from scipy.stats import bernoulli
fig,axes = plt.subplots(1,2,figsize=(12,4))
r = bernoulli(p=0.6) # 生成伯努利分布
plot_distribution(r,axes)
array([<matplotlib.axes._subplots.AxesSubplot object at 0x00000277A9C8B8E0>,
<matplotlib.axes._subplots.AxesSubplot object at 0x00000277A9CB3100>],
dtype=object)
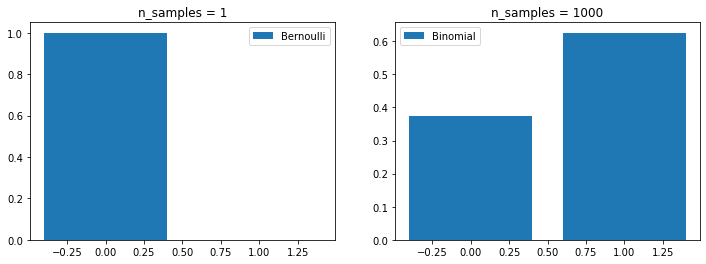
# 生成实验成功的次数
p = 0.6
def trials(n_samples):
# 二项分布,n_samples表示实验次数,p表示成功的概率,samples表示成功的次数
samples = np.random.binomial(n_samples,p)
proba_zero = (n_samples-samples)/n_samples# 0次成功的概率
proba_one = samples/n_samples# 1次成功的概率
return [proba_zero,proba_one]
fig,axes = plt.subplots(1,2,figsize=(12,4))
# 一次实验,伯努利分布
n_samples = 1
axes[0].bar([0,1],trials(n_samples),label ='Bernoulli')
axes[0].set_title('n_samples = {}'.format(n_samples))
# n次实验,二项分布
n_samples = 1000
axes[1].bar([0,1],trials(n_samples),label ='Binomial')
axes[1].set_title('n_samples = {}'.format(n_samples))
for ax in axes:
ax.legend()
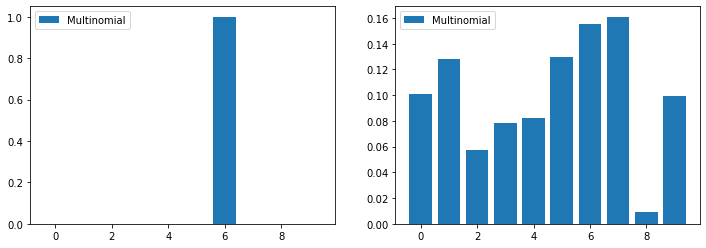
范畴分布(Categorical distribution,分类分布)是一个多项分布的特例,它的概率质量函数是(表示第k类的概率):
\(P(X=k)=p_k\)
例如每次试验的结果就可以表示成一个k维的向量,每个维度表示一种结果,只有此次试验的结果对应的维度为1,其余维度为0,例如:
\(P(X=(1,0,0,0))=p_1\)
\(P(X=(0,1,0,0))=p_2\)
\(P(X=(0,0,1,0))=p_3\)
\(P(X=(0,0,0,1))=p_4\)
def k_possibilities(k):
'''生成k个可能的结果'''
res = np.random.rand(k)# random.rand(k)生成k个[0,1)之间的随机数
_sum = sum(res) # 求和
for i,x in enumerate(res):
res[i] = x/_sum # 归一化,enumerate返回索引和值,i表示索引,x表示值
return res
fig,axes = plt.subplots(1,2,figsize=(12,4))
# 一次实验,范畴分布
n_samples = 1
k=10
samples = np.random.multinomial(n_samples,k_possibilities(k))
axes[0].bar(range(len(samples)),samples/n_samples,label ='Multinomial')
# n次实验,多项分布
n_samples = 1000
samples = np.random.multinomial(n_samples,k_possibilities(k))
axes[1].bar(range(len(samples)),samples/n_samples,label ='Multinomial')
for ax in axes:
ax.legend()
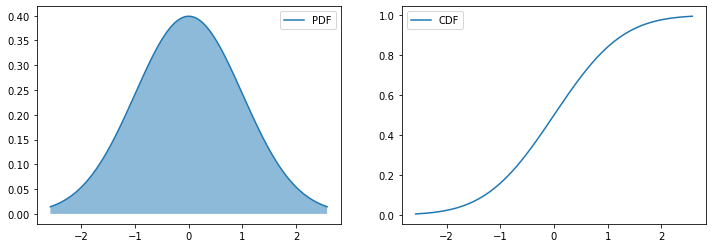
高斯分布(Gaussian distribution,正态分布)是一个连续型概率分布,若随机变量$X\sim \mathcal{N}(\mu,\sigma^2)$,它的概率密度函数是:
\(P(X=x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
有时也会用$\beta = \frac{1}{\sigma^2}$来表示分布的精度(精度越大,分布越狭窄,precision):
\(P(X=x)=\frac{1}{\sqrt{2\pi\beta^{-1}}}e^{-\frac{(x-\mu)^2}{2\beta}}\)
中心极限定理(central limit theorem)是一个重要的定理,它表示当样本量足够大时,样本均值的分布会趋近于正态分布,如噪声的分布就是一个典型的例子,噪声的分布是均匀分布,但是当噪声的数量足够多时,噪声的均值的分布就会趋近于正态分布。
如果我们对随机变量进行标准化,即将随机变量减去均值并除以标准差,那么标准化后的随机变量的均值为0,标准差为1,这样的随机变量称为标准正态分布(standard normal distribution),
\(Z=\frac{X-\mu}{\sigma}\)
from scipy.stats import norm
fig,axes = plt.subplots(1,2,figsize= (12,4))
mu,sigma = 0,1# 均值,标准差
r = norm(loc=mu,scale=sigma)# 生成正态分布
plot_distribution(r,axes) #绘制r的PDF和CDF
array([<matplotlib.axes._subplots.AxesSubplot object at 0x000001B387029910>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001B386E8E430>],
dtype=object)
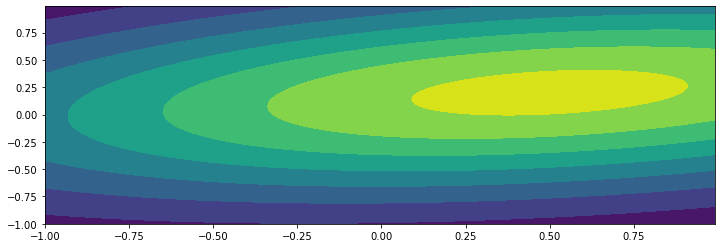
多元高斯分布(multivariate Gaussian distribution)是一个多维的高斯分布,它的概率密度函数是:
\(P(X=x;\sigma,\Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}\)
具体推导过程如下:
先假设 $\mathrm{n}$ 个变量 $x=\left[x_1, x_2, \cdots, x_n\right]^{\mathrm{T}}$ 互不相关,且服从正态分布 (维度不相关多元正态分布),各个维度的均值 $E(x)=\left[\mu_1, \mu_2, \cdots, \mu_n\right]^{\mathrm{T}}$ ,方差 $\sigma(x)=\left[\sigma_1, \sigma_2, \cdots, \sigma_n\right]^{\mathrm{T}}$
根据联合概率密度公式:
\(\begin{aligned}
& f(x)=p\left(x_1, x_2 \ldots x_n\right)=p\left(x_1\right) p\left(x_2\right) \ldots p\left(x_n\right)=\frac{1}{(\sqrt{2 \pi})^n \sigma_1 \sigma_2 \cdots \sigma_n} e^{-\frac{\left(x_1-\mu_1\right)^2}{2 \sigma_1^2}-\frac{\left(x_2-\mu_2\right)^2}{2 \sigma_2^2} \cdots-\frac{\left(x_n-\mu_n\right)^2}{2 \sigma_n}} \\
& \text { 令 } z^2=\frac{\left(x_1-\mu_1\right)^2}{\sigma_1^2}+\frac{\left(x_2-\mu_2\right)^2}{\sigma_2^2} \cdots+\frac{\left(x_n-\mu_n\right)^2}{\sigma_n^2}, \sigma_z=\sigma_1 \sigma_2 \cdots \sigma_n
\end{aligned}\)
这样多元正态分布又可以写成一元那种漂亮的形式了(注意一元与多元的差别):
\(f(z)=\frac{1}{(\sqrt{2 \pi})^n \sigma_z} e^{-\frac{z^2}{2}}\)
因为多元正态分布有着很强的几何思想,单纯从代数的角度看待z很难看出 z的概率分布规律,这里需要转换成矩阵形式:
\(z^2=z^{\mathrm{T}} z=\left[x_1-\mu_1, x_2-\mu_2, \cdots, x_n-\mu_n\right]\left[\begin{array}{cccc}
\frac{1}{\sigma_1^2} & 0 & \cdots & 0 \\
0 & \frac{1}{\sigma_2^2} & \cdots & 0 \\
\vdots & \cdots & \cdots & \vdots \\
0 & 0 & \cdots & \frac{1}{\sigma_n^2}
\end{array}\right]\left[x_1-\mu_1, x_2-\mu_2, \cdots, x_n-\mu_n\right]^{\mathrm{T}}\)
等式比较长,让我们要做一下变量替换:
\(x-\mu_x=\left[x_1-\mu_1, x_2-\mu_2, \cdots, x_n-\mu_n\right]^{\mathrm{T}}\)
定义一个符号
\(\sum=\left[\begin{array}{cccc}
\sigma_1^2 & 0 & \cdots & 0 \\
0 & \sigma_2^2 & \cdots & 0 \\
\vdots & \cdots & \cdots & \vdots \\
0 & 0 & \cdots & \sigma_n^2
\end{array}\right]\)
$\sum$ 代表变量 $\mathrm{X}$ 的协方差矩阵, i行j列的元素值表示 $x_i$ 与 $x_j$ 的协方差
因为现在变量之间是相互独立的,所以只有对角线上 $(i=j)$ 存在元素,其他地方都等于 0 ,且 $x_i$ 与它本身的协方差就等于方差。
$\sum$ 是一个对角阵,根据对角矩阵的性质,它的逆矩阵:
\(\left(\sum\right)^{-1}=\left[\begin{array}{cccc}
\frac{1}{\sigma_1^2} & 0 & \cdots & 0 \\
0 & \frac{1}{\sigma_2^2} & \cdots & 0 \\
\vdots & \cdots & \cdots & \vdots \\
0 & 0 & \cdots & \frac{1}{\sigma_n^2}
\end{array}\right].\)
对角矩阵的行列式 $=$ 对角元素的乘积
\(\sigma_z=\left|\sum\right|^{\frac{1}{2}}=\sigma_1 \sigma_2 \ldots \sigma_n\)
替换变量之后,等式可以简化为:
\(z^{\mathrm{T}} z=\left(x-\mu_x\right)^{\mathrm{T}} \sum^{-1}\left(x-\mu_x\right)\)
代入以z为自变量的标准高斯分布函数中:
\(f(z)=\frac{1}{(\sqrt{2 \pi})^n \sigma_z} e^{-\frac{z^2}{2}}=\frac{1}{(\sqrt{2 \pi})^n \sum^{\frac{1}{2}}} e^{-\frac{\left(x-\mu_x\right)^T(\Gamma)^{-1}\left(x-\mu_x\right)}{2}}\)
注意前面的系数变化: 从非标准正态分布 $->$ 标准正态分布需要将概率密度函数的高度压缩 $\left|\sum\right|^{\frac{1}{2}}$ 倍,从一维 $\rightarrow$ n维的过 程中,每增加一维,高度将压缩 $\sqrt{2 \pi}$ 倍
reference: https://www.cnblogs.com/bingjianing/p/9117330.html
from scipy.stats import multivariate_normal
x,y = np.mgrid[-1:1:.01,-1:1:.01]# 生成网格点,步长为0.01
pos = np.dstack((x,y))# 生成网格点坐标,shape=(200,200,2)
sigma = [[2,0.3],[0.3,0.5]] # 协方差矩阵
mu = [0.5,0.2]
X = multivariate_normal(mu,sigma)# 生成多元正态分布
fig,axes = plt.subplots(1,1,figsize=(12,4))
axes.contourf(x,y,X.pdf(pos))# 绘制等高线,pos表示在网格点上的概率密度
<matplotlib.contour.QuadContourSet at 0x1b386e185b0>
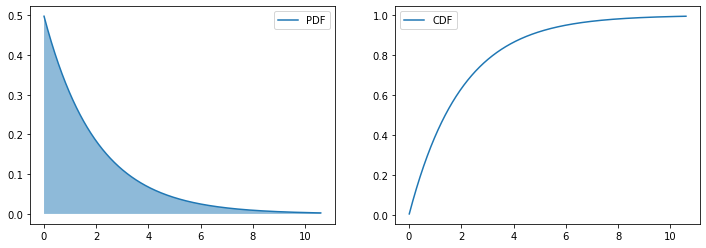
指数分布(Exponential distribution)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟,它具有无记忆(Memoryless Property)的关键性质,也即是$P(T>t+s|T>t)=P(T>s)$。
除了用于分析泊松过程外,还可以在其他各种环境中找到,其概率密度函数为:
\(p(x)=\left\{\begin{array}{c}
\frac{1}{\theta} e^{-\frac{x}{\theta}}, x>0 \\
0, x \leq 0
\end{array} \quad(\theta>0)\right.\)
则称随机变量$X$ 服从参数为 $\theta$ 的指数分布, 记为 $X \sim \operatorname{EXP}(\theta)$.
其中 $\lambda = \frac{1}{\theta}$ 称为率参数(rate parameter)。
即每单位时间内发生某事件的次数(比方说:如果你平均每个小时接到2次电话,那么你预期等待每一次电话的时间是半个小时)。指数分布的期望和方差分别为 $\theta$ 和 $\theta^2$.
指数分布的累计分布函数为:
\(P(X \leq x) = 1 - e^{-\frac{x}{\theta}}\)
from scipy.stats import expon
fig,axes = plt.subplots(1,2,figsize=(12,4))
r = expon(scale=2)# 生成指数分布,scale=2表示λ=1/2
plot_distribution(r,axes)
array([<matplotlib.axes._subplots.AxesSubplot object at 0x000001B387102DF0>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001B387165340>],
dtype=object)
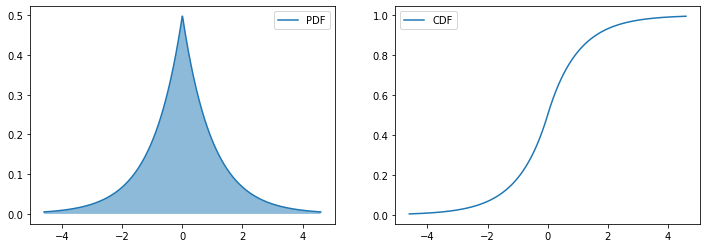
拉普拉斯分布(Laplace distribution)是一种连续概率分布,它是双指数分布的特殊情况。它是一种对称分布,其概率密度函数为:
\(p(x) = \frac{1}{2 \lambda} e^{ - \frac{|x - \mu|}{\lambda}}\)
其中 $\mu$ 称为分布的位置参数(location parameter),$\lambda$ 称为分布的尺度参数(scale parameter)。拉普拉斯分布的期望和方差分别为 $\mu$ 和 $2 \lambda^2$.
from scipy.stats import laplace
fig,axes = plt.subplots(1,2,figsize=(12,4))
mu,gamma = 0,1 # 均值,标准差
r = laplace(loc=0,scale=1)# 生成拉普拉斯分布
plot_distribution(r,axes)
array([<matplotlib.axes._subplots.AxesSubplot object at 0x000001B3870DF130>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001B385D4DE20>],
dtype=object)
Dirac 分布:Dirac delta function,也称为 Dirac 分布。
Dirichlet分布 基础知识:conjugate priors共轭先验 共轭先验是指这样一种概率密度:它使得后验概率的密度函数与先验概率的密度函数具有相同的函数形式。它极大地简化了贝叶斯分析。 如何解释这句话。由于$P(u|D) = p(D|u)p(u)/p(D)$,其中D是给定的一个样本集合,因此对其来说p(D)是一个确定的值,可以理解为一个常数。P(u|D)是后验概率—-即观察到一系列样本数据后模型参数服从的概率,p(D|u)是似然概率—-在给定的模型参数u下样本数据服从这一概率模型的相似程度,p(u)是u的先验概率—-在我们一无所知的情况下u的概率分布。P(u|D)的函数形式完全由p(D|u)和p(u)的乘积决定。如果p(u)的取值使p(u|D)和p(D|u)相同的表达形式(关于u的表达形式),就称p(u)为共轭先验。
reference:
机器学习的数学基础(1)–Dirichlet分布
Beta分布式二项分布的共轭先验分布.
Dirichlet分布是一个多维的概率分布,它是一组(多元)独立的 $\operatorname{Beta}$ 分布的共轭先验分布。在贝叶斯推断(Bayesian inference)中,狄利克雷分布作为多项分布的共轭先验得到应用,在机器学习(machine learning)中被用于构建狄利克雷混合模型(Dirichlet mixture model)是一类在实数域以正单纯形(standard simplex)为 支撑集(support)的高维连续概率分布,是Beta分布在高维情形的推广。
reference:
理解Gamma分布、Beta分布与Dirichlet分布
最通俗易懂的白话狄利克雷过程(Dirichlet Process)
2.1.6 常见函数的有用性质
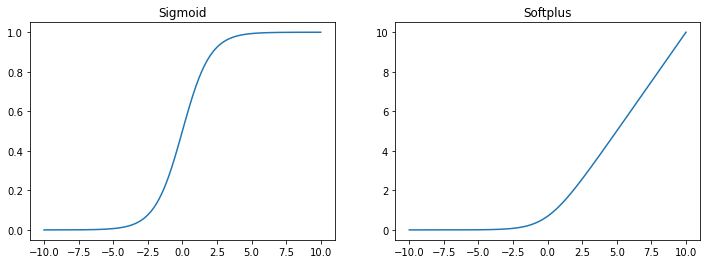
logisitc sigmoid函数通常用来产生伯努利分布的概率,因为它的范围是 (0, 1),因此它的导数是伯努利分布的概率密度函数。sigmoid 函数在变量取绝对值⾮常⼤的正值或负值时会出现饱和 (Saturate)现象,意味着函数会变得很平,并且对输⼊的微⼩改变会变得不敏感。
\(sigmoid(x) = \frac{1}{1+e^{-x}}\)
softplus函数
\(softplus(x) = \log(1+e^x)\)
因为它的范围是 (0, ∞),softplus函数可以用来产生正太分布的$\beta$和$\sigma$参数,因此它的导数是正太分布的概率密度函数。 softplus函数名称来源于它是一个平滑的ReLU函数,ReLU函数是一个非线性函数,它的定义是 \(ReLU(x) = max(0, x)\)
x = np.linspace(-10,10,1000)
sigmoid = 1/(1+np.exp(-x))
softplus = np.log(1+np.exp(x))
fig,axes = plt.subplots(1,2,figsize=(12,4))
axes[0].plot(x,sigmoid)
axes[0].set_title('Sigmoid')
axes[1].plot(x,softplus)
axes[1].set_title('Softplus')
Text(0.5, 1.0, 'Softplus')
2.2 信息论
信息论背后的思想:一件不太可能的事件比一件比较可能的事件更有信息量。(信息量的度量就等于不确定性的多少。)
信息 (Information) 需要满⾜的三个条件:
- ⽐较可能发⽣的事件的信息量要少
- ⽐较不可能发⽣的事件的信息量要⼤
- 独⽴发⽣的事件之间的信息量应该是可以叠加的。例如,投掷的硬币两次正⾯朝上传递的信息量,应该是投掷⼀次硬币正⾯朝上的信息量的两倍
自信息 (Self-information) 是信息论中的基本概念,它是指单个事件发⽣的信息量。自信息的定义是
\(I(x) = -\log P(x)\)
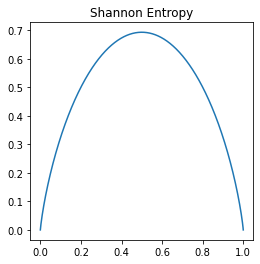
香农熵 (Shannon Entropy)是对于整个概论分布P,随机变量的不确定性的衡量:
\(H(P) = -( p_1 * \log p_1 + p_2 * \log p_2 + \cdots + p_n * \log p_n) =-\sum_{x}P(x)\log P(x)\)
联合熵 (Joint Entropy) 是对于两个随机变量X和Y,它们的联合分布P(X, Y),随机变量的不确定性的衡量:
\(H(X, Y) = -\sum_{x,y}P(x, y)\log P(x, y)\)
条件熵 (Conditional Entropy) 是对于两个随机变量X和Y,它们的联合分布P(X, Y),随机变量的不确定性的衡量:
\(H(Y|X) = -\sum_{x,y}P(x, y)\log P(y|x)\)
互信息 (Mutual Information) 表示两个信息相交的部分:
\(I(X;Y) = H(X)+H(Y) - H(X,Y)\)
信息变差(Variation of Information) 表示两个事件的信息不想交的部分:
\(VI(X;Y) = H(X)+H(Y) - 2I(X;Y)\)
p = np.linspace(1e-6,1-1e-6,1000) # 生成概率
entropy = -p*np.log(p)-(1-p)*np.log(1-p) # 香农熵 (Shannon Entropy)
plt.figure(figsize=(4,4))
plt.plot(p,entropy)
plt.title('Shannon Entropy')
Text(0.5, 1.0, 'Shannon Entropy')
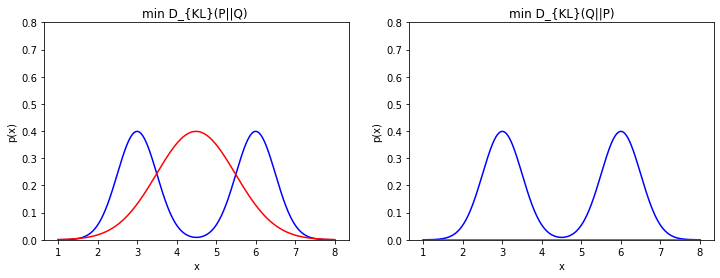
信息增益(Kullback–Leibler divergence)又称information divergence,information gain,relative entropy 或者KLIC。
在概率论和信息论中,信息增益是非对称的,用以度量两种概率分布P和Q的差异。
\(D_{KL}(P||Q) = \sum_{x}P(x)\log \frac{P(x)}{Q(x)}\)
交叉熵 (Cross Entropy) 假设P是真实的分布,Q是预测的分布,那么交叉熵就是真实分布和预测分布之间的距离:
\(H(P, Q) = H(P) + D_{KL}(P||Q) = -\sum_{x}P(x)\log Q(x)\)
# D_{KL}(P||Q) 与D_{KL}(Q||P)比较
x = np.linspace(1,8,500)
y1 = norm.pdf(x,loc =3,scale = 0.5) # loc=3,scale=0.5表示均值为3,标准差为0.5
y2 = norm.pdf(x,loc =6,scale = 0.5)
p = y1+y2 #构造p(x)
KL_pq ,KL_qp = [],[]
q_list = []
for mu in np.linspace(0,10,50):
for sigma in np.linspace(0.1,1,50): # 生成50*50个q(x),寻找最优q(x)
q = norm.pdf(x,loc =mu,scale = sigma) # 构造q(x)
q_list.append(q)
KL_pq.append(np.sum(p*np.log(p/q))) # D_{KL}(P||Q)
KL_qp.append(np.sum(q*np.log(q/p))) # D_{KL}(Q||P)
# min
min_KL_pq = np.argmin(KL_pq) # 最小值的索引
min_KL_qp = np.argmin(KL_qp)
fig,axes = plt.subplots(1,2,figsize=(12,4))
axes[0].set_ylim(0,0.8)
axes[0].plot(x,p/2,'b',label='p(x)')
axes[0].plot(x,q_list[min_KL_pq],'r',label='$q^*(x)$')
axes[0].set_title('min D_{KL}(P||Q) ')
axes[0].set_xlabel('x')
axes[0].set_ylabel('p(x)')
axes[1].set_ylim(0,0.8)
axes[1].plot(x,p/2,'b',label='p(x)')
axes[1].plot(x,q_list[min_KL_qp],'r',label='$q^*(x)$')
axes[1].set_title('min D_{KL}(Q||P)')
axes[1].set_xlabel('x')
axes[1].set_ylabel('p(x)')
<ipython-input-60-0ceffff0da69>:12: RuntimeWarning: divide by zero encountered in true_divide
KL_pq.append(np.sum(p*np.log(p/q))) # D_{KL}(P||Q)
<ipython-input-60-0ceffff0da69>:12: RuntimeWarning: overflow encountered in true_divide
KL_pq.append(np.sum(p*np.log(p/q))) # D_{KL}(P||Q)
<ipython-input-60-0ceffff0da69>:13: RuntimeWarning: divide by zero encountered in log
KL_qp.append(np.sum(q*np.log(q/p))) # D_{KL}(Q||P)
<ipython-input-60-0ceffff0da69>:13: RuntimeWarning: invalid value encountered in multiply
KL_qp.append(np.sum(q*np.log(q/p))) # D_{KL}(Q||P)
Text(0, 0.5, 'p(x)')
信息增益 (Information Gain) 是指在知道特征X的条件下,特征Y的不确定性减少的程度:
\(IG(X;Y) = H(Y) - H(Y|X)\)
import numpy as np
import pandas as pd
from math import log
def create_data():
datasets = [['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets, labels
# 熵
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p / data_length) * log(p / data_length, 2) for p in label_count.values()])
return ent
# 经验条件熵
def cond_ent(datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()])
return cond_ent
# 信息增益
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gain_train(datasets):
count = len(datasets[0]) - 1
ent = calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])
datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
print(train_data)
print('特征信息增益为:', info_gain_train(np.array(datasets)))
年龄 有工作 有自己的房子 信贷情况 类别
0 青年 否 否 一般 否
1 青年 否 否 好 否
2 青年 是 否 好 是
3 青年 是 是 一般 是
4 青年 否 否 一般 否
5 中年 否 否 一般 否
6 中年 否 否 好 否
7 中年 是 是 好 是
8 中年 否 是 非常好 是
9 中年 否 是 非常好 是
10 老年 否 是 非常好 是
11 老年 否 是 好 是
12 老年 是 否 好 是
13 老年 是 否 非常好 是
14 老年 否 否 一般 否
特征(年龄) - info_gain - 0.083
特征(有工作) - info_gain - 0.324
特征(有自己的房子) - info_gain - 0.420
特征(信贷情况) - info_gain - 0.363
特征信息增益为: 特征(有自己的房子)的信息增益最大,选择为根节点特征
2.3 图模型
图模型(Graphical Model)是一种表示概率分布的方法,它将概率分布表示为一个图,图中的节点表示随机变量,节点之间的边表示随机变量之间的依赖关系。
2.3.1 有向图模型 directed graphical model
有向图模型是指图中的边是有向的,即边的方向表示了随机变量之间的依赖关系。有向图模型可以表示条件概率分布(CPD),也可以表示马尔科夫随机场。
有向图的代表是贝叶斯网。 贝叶斯⽹与朴素贝叶斯模型建⽴在相同的直观假设上:通过利用分布的条件独立性来获得紧凑而自然的表示。贝叶斯⽹核⼼是⼀个有向⽆环图(DAG),其节点为论域中的随机变量,节点间的有向箭头表⽰这两个节点的依赖关系。
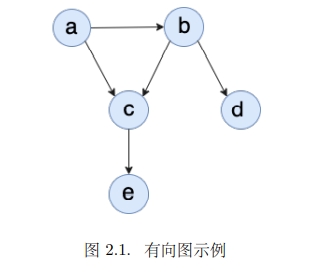
有向⽆环图可以由如下 3 种元结构构成:
- 同⽗结构
- V 型结构
- 顺序结构
贝叶斯网的独立性
- 局部独立性
- 全局独立性
- tail-to-tail
- head-to-tail
- head-to-head
考虑复杂的有向无环图,如果A,B,C是三个集合,可以是单独的节点或者节点的集合。为了判断A和B是否时C条件独立的,我们可以考虑A和B之间的所有路径。对于其中的一条路径,如果满足以下两点的任意一点,那么就说这条路径是阻塞(blocked)的:
- 路径中存在某个节点 X 是 head-to-tail 或者 tail-to-tail 节点,并且 X 是包含在 C 中的;
- 路径中存在某个节点 X 是 head-to-head 节点,并且 X 或 X 的⼉⼦是不包含在 C 中的。
如果 A,B 间所有的路径都是阻塞的,那么 A,B 就是关于 C 条件独⽴的;否则 A,B 不是关于 C 条件独⽴的。
import networkx as nx
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
import matplotlib.pyplot as plt
%matplotlib inline
# 建立一个简单贝叶斯模型框架
model = BayesianModel([('a', 'b'), ('a', 'c'), ('b', 'c'), ('b', 'd'), ('c', 'e')])
# 最顶层的父节点的概率分布表
cpd_a = TabularCPD(variable='a', variable_card=2, values=[[0.6, 0.4]]) # a: (0,1)
# 其它各节点的条件概率分布表(行对应当前节点索引,列对应父节点索引)
cpd_b = TabularCPD(variable='b', variable_card=2, # b: (0,1)
values=[[0.75, 0.1],
[0.25, 0.9]],
evidence=['a'],
evidence_card=[2])
cpd_c = TabularCPD(variable='c', variable_card=3, # c: (0,1,2)
values=[[0.3, 0.05, 0.9, 0.5],
[0.4, 0.25, 0.08, 0.3],
[0.3, 0.7, 0.02, 0.2]],
evidence=['a', 'b'],
evidence_card=[2, 2])
cpd_d = TabularCPD(variable='d', variable_card=2, # d: (0,1)
values=[[0.95, 0.2],
[0.05, 0.8]],
evidence=['b'],
evidence_card=[2])
cpd_e = TabularCPD(variable='e', variable_card=2, # e: (0,1)
values=[[0.1, 0.4, 0.99],
[0.9, 0.6, 0.01]],
evidence=['c'],
evidence_card=[3])
# 将各节点的概率分布表加入网络
model.add_cpds(cpd_a, cpd_b, cpd_c, cpd_d, cpd_e)
# 验证模型数据的正确性
print(u"验证模型数据的正确性:",model.check_model())
# 绘制贝叶斯图 (节点 + 依赖关系)
nx.draw(model, with_labels=True, node_size=1000, font_weight='bold', node_color='y', \
pos={"e":[4,3],"c":[4,5],"d":[8,5],"a":[2,7],"b":[6,7]})
plt.text(2,7,model.get_cpds("a"), fontsize=10, color='b')
plt.text(5,6,model.get_cpds("b"), fontsize=10, color='b')
plt.text(1,4,model.get_cpds("c"), fontsize=10, color='b')
plt.text(4.2,2,model.get_cpds("e"), fontsize=10, color='b')
plt.text(7,3.4,model.get_cpds("d"), fontsize=10, color='b')
plt.show()
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
<ipython-input-1-96c0e1595c11> in <module>
1 import networkx as nx
----> 2 from pgmpy.models import BayesianModel
3 from pgmpy.factors.discrete import TabularCPD
4 import matplotlib.pyplot as plt
5 get_ipython().run_line_magic('matplotlib', 'inline')
ModuleNotFoundError: No module named 'pgmpy'
2.3.2 无向图模型 (Undirected Model)
马尔可夫网节点间的依赖关系是无向的(相互平等的关系),⽆法⽤条件概率分布来表⽰,为此为引⼊极大团概念,进⽽为每个极⼤团引⼊⼀个势函数作为因⼦,然后将联合概率分布表⽰成这些因⼦的乘积再归⼀化,归⼀化常数被称作配分函数。





