主要包括使用一维卷积神经网络(1D CNN)对安装在远程风机的高速轴承中的现场传感器采集到的时间序列数据通过短时傅里叶变化之后得到的频谱峰度(Kurtosis Spectogram)进行分类,得到每个样品的类别:中等寿命级(预期寿命大于15天的轴承——状态良好)以及短寿命轴承(预期寿命小于15天的轴承——状态不良)。
原文链接:Wind Turbine High Speed Bearing Prognosis Kaggle
1. 问题描述
本文展示了使用振动监测传感器的原始数据来预测轴承的RUL(剩余使用寿命)的新方法,这种方法也可以用于其他类型的机器元件,如齿轮、联轴器等剩余寿命的预测。
本例中使用的数据是由安装在一个远程风力涡轮机的高速轴承上的现场传感器记录的。 该轴承是齿轮箱的一部分,负责转子和发电机之间的耦合,特别是在高速轴上(发电机一侧)。
该数据可以通过以下方式访问:
记录的变量是传感器在30天内测得的加速度(单位:g),每天6秒。
2. 技术背景
该方法是基于对50个样本中的每个样本的Kurtosis Spectogram(频谱峰度)的计算,并使用1D-CNN–一维卷积神经网络将每个样本划分为两个RUL等级。中等预期寿命类,代表轴承的预期寿命大于15天(状况良好)。
- 中等预期寿命的类别:寿命大于15天(状况良好)。
- 短预期寿命类别,代表轴承的寿命期望值小于15天(状况不佳)。
基于这个假设,寿命最短的15个被标记为短寿命类,而所有剩余的被标记为中寿命类。
数据处理流程
导入包
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['mathtext.fontset'] = 'stix'
matplotlib.rcParams['font.family'] = 'sans-serif'
matplotlib.rcParams['font.size'] = 10
from scipy.io import loadmat # scipy加载mat文件
from scipy.signal import stft # scipy的短时傅里叶变换
from scipy.stats import kurtosis # kurtosis表示峰度,峰度是统计学中的一个概念,用来描述某个分布的峰值的陡峭程度
from mpl_toolkits.mplot3d import Axes3D
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import *
from tensorflow.keras.layers import *
from tensorflow.keras.utils import *
定义混淆矩阵可视化函数
def plotConfusionMatrix(dtrue,dpred,classes,\
cmap = plt.cm.Blues,bsize = 1.0): # 混淆矩阵可视化函数,dtrue表示真实值,dpred表示预测值,classes表示类别,cmap表示颜色,bsize表示图像大小
cm = confusion_matrix(dtrue,dpred,normalize = 'true') # 混淆矩阵,normalize = 'true'表示归一化
fig,ax = plt.subplots(figsize = (np.shape(classes)[0] * 1.25 * bsize,\
np.shape(classes)[0] * 1.25 * bsize))
im = ax.imshow(cm,interpolation = 'nearest',cmap = cmap) # interpolation = 'nearest'表示插值方式,nearest表示最近邻插值,cm表示混淆矩阵,cmap表示颜色
ax.set(xticks = np.arange(cm.shape[1]),\
yticks = np.arange(cm.shape[0]),\
xticklabels = classes,\
yticklabels = classes,\
ylabel = 'True Efficiency',\
xlabel = 'Predicted Efficiency')
plt.setp(ax.get_xticklabels(),rotation = 90,ha = 'right',\
rotation_mode = 'anchor') # ha表示水平对齐方式,rotation_mode表示旋转模式,anchor表示锚点;setp表示设置属性
fmt = '.2f' # 保留两位小数
thresh = cm.max() / 2.0
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j,i,format(cm[i,j],fmt),ha = 'center',va = 'center',\
color = 'white' if cm[i,j] > thresh else 'black') # ha表示水平对齐方式,va表示垂直对齐方式,j表示列,i表示行
fig.tight_layout()
return ax
查看数据
扫描频率为97656HZ,采样的总共时长为6s,所以采样点的个数为
fname = !ls './input/data'
fname = np.asarray(fname)
df = []
for i in fname:
df.append(loadmat('./input/data/' + i)['vibration'].flatten())# loadmat表示加载mat文件,flatten表示降维
df = np.asarray(df) # 转换为数组
df.shape[0]
输出结果为:
50 # 表示样本数量
查看采样频率
fs = int(df.shape[1] / 6.0) # 采样频率
t = np.linspace(0.0,6.0,df.shape[1]) # df.shape[1]表示df的第二维度的长度,即采样点数;t表示一个周期内,每个采样点的时间;
print('Scan frequency: {:,d} Hz'.format(fs)) # {:,d}表示以逗号分隔的十进制整数,scan frequency表示扫描频率
输出结果为:
Scan frequency: 97,656 Hz
下图显示了加速度的测量值(单位:g),正如可以注意到的那样,加速度的振幅在时域上变化明显(x轴表示时间,每天6秒,50天)
plt.subplots(figsize = (12.0,6.0))
for i in range(df.shape[0]):
plt.plot(t + i * 6.0,df[i],color = 'black',lw = 0.25)
plt.xlabel('Time (in s): sample = 50 days in total, 6 seconds per day')
plt.ylabel('Acceleration (in g)')
plt.show()
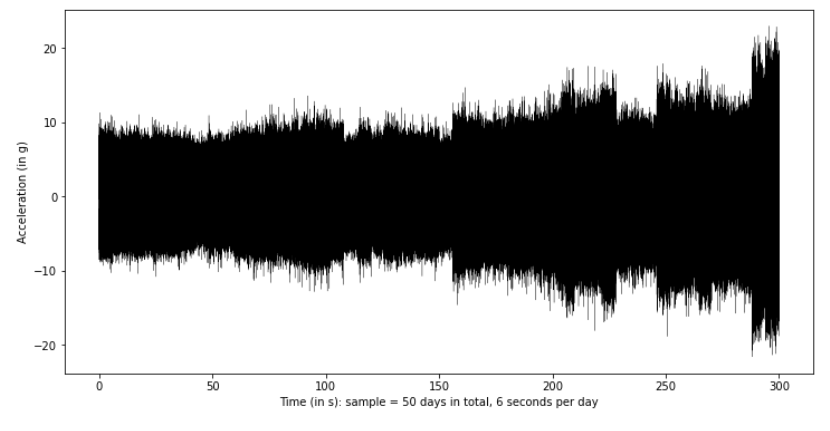
尽管加速度有明显的变化,记录的数据数量(6 x 97,656 = 每天585,936个记录;总共29,286,800个)很大,再加上 测量的非同步条件,使得使用传统的神经网络来对轴承状况进行分类是不可行的。
这个问题需要一个不同的方法来将正弦波的时域变量转化为非周期性变量,从而使区分RUL等级成为可能。
Kurtosis
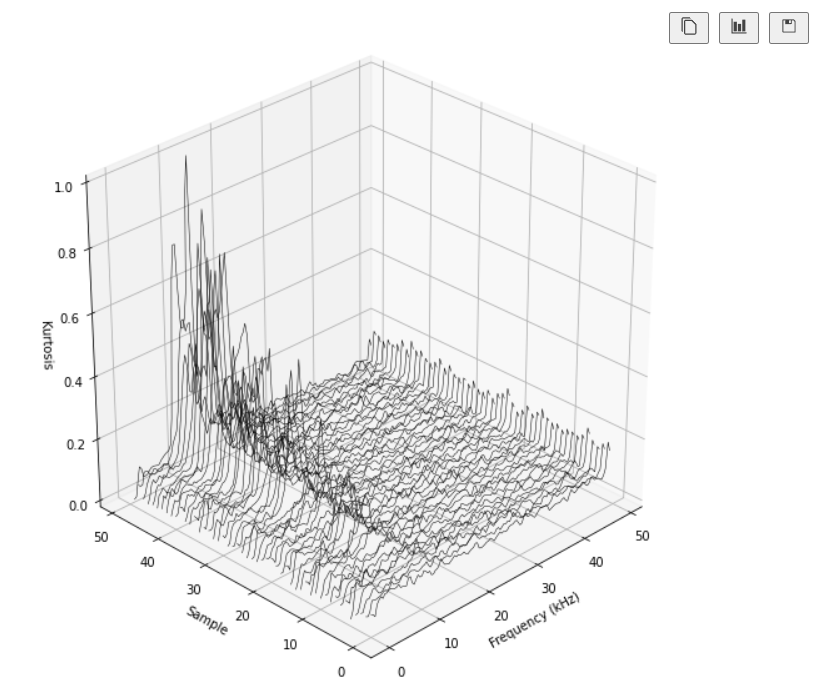
这个新的变量是通过短时傅里叶变换计算的Kurtosis,如下图所示的三维图。可以注意到,在正常情况下,Kurtosis是非常稳定的,无论频率如何变化(例如前五个样本),但当异常的运行条件导致数据偏离正态分布时,则Kurtosis趋于变大。
f = []
fft = []
wnd = 127
for i in range(df.shape[0]):
u,v,w = stft(df[i],fs,nperseg = wnd,noverlap = int(0.8 * wnd),nfft = int(2.0 * wnd))
# stft表示短时傅里叶变换,fs表示采样频率;nperseg表示每段的长度,
# noverlap表示重叠的长度,nfft表示fft的长度
# u表示频率,v表示时域,w表示频谱
f.append(u)
fft.append(kurtosis(np.abs(w),fisher = False,axis = 1)) # 对频谱取绝对值,然后计算峰度
# fisher表示是否使用Fisher标准化,axis = 1表示沿着第二维度计算峰度
f = np.asarray(f) # asarray表示将输入转换为数组,f表示频率
fft = np.asarray(fft)
fftn = (fft - fft.min()) / (fft.max() - fft.min()) # 归一化,n表示归一化后的频谱
fftn = np.asarray(fftn)
n = np.ones_like(f[0])# ones_like表示返回与输入形状相同的数组,数组元素为1
fig = plt.figure(figsize = (10.0,10.0))
ax = plt.axes(projection = '3d')
ax.view_init(30,225)
for i in range(f.shape[0]):
ax.plot(f[i] / 1.0e3,i * n,fftn[i],color = 'black',linewidth = 0.50) # / 1.0e3表示将频率转换为kHz
ax.set_xlabel('Frequency (kHz)')
ax.set_ylabel('Sample')
ax.set_zlabel('Kurtosis')
plt.show()
模型训练
准备模型
Kurtosis被用作1D-CNN的输入(变量x),而与两个RUL等级相关的标签则通过变量y–中寿命期望值类(y = 0)用于前35个样本,而短寿命预期类(y = 1)用于最后15个样本。 y被转换为分类格式,以适应神经网络的输出格式。
1D-CNN是通过使用Keras开源库的Sequential()函数定义的。
X = fftn
X = X.reshape(-1,f.shape[1],1) # reshape表示改变数组的形状,-1表示自动计算,1表示一维,f.shape[1]表示频率的长度
y = np.zeros(X.shape[0],dtype = int)
y[-15:] = 1 # y表示标签,-15表示从后往前数第15个,都是short-life expectancy class (y = 1)
print('Input shape: {:d} samples x {:d} registers/sample'.format(X.shape[0],X.shape[1]))
label = to_categorical(y) # to_categorical表示将标签转换为one-hot编码,one-hot编码表示将标签转换为二进制向量
label
Input shape: 50 samples x 128 registers/sample
mdl = Sequential() # Sequential表示顺序模型
mdl.add(Conv1D(100,6,activation = 'relu',\
input_shape = (f.shape[1],1))) # Conv1D表示一维卷积层,100表示卷积核的个数,6表示卷积核的大小,activation表示激活函数
mdl.add(Conv1D(100,6,activation = 'relu'))
mdl.add(MaxPooling1D(3))
mdl.add(Conv1D(160,6,activation = 'relu'))
mdl.add(Conv1D(160,6,activation = 'relu'))
mdl.add(GlobalAveragePooling1D())
mdl.add(Dropout(0.5))
mdl.add(Dense(2,activation = 'softmax'))
print(mdl.summary())
输出结果如下:

训练模型
mdl.compile(loss = 'categorical_crossentropy',\
optimizer = 'adam',metrics = ['accuracy']) # compile表示编译模型,loss表示损失函数,optimizer表示优化器,metrics表示评估模型的指标
该模型在50%的样本上进行了训练–需要注意的是,该数据集非常有限,只有50个样本,尽管每个样本有大量的记录。
训练是基于1,000个epochs–这是为了让模型有一个良好的收敛。
代价矩阵(变量cw)被用来影响分类结果并避免与错误分类相关的错误。
当遇到很难决策的时候,将中等寿命的轴承归类为短寿命轴承,并将决定权交给维修专家,让维修专家来决定,而不是错误地将短寿命的轴承错误分类并导致机组故障。
batch,epoch = 32,1000 # batch表示每次训练的样本数,epoch表示训练的轮数
cw = {0: 5.0,1:75.0} # cw表示类别权重
Xtrain,Xtest,ytrain,ytest = train_test_split(X,label,\
random_state = 21,\
test_size = 0.50)
# train_test_split表示将数据集分为训练集和测试集,random_state表示随机数种子,test_size表示测试集的比例为50%
hist = mdl.fit(Xtrain,ytrain,batch_size = batch,\
epochs = epoch,validation_split = 0.2,verbose = 0,\
class_weight = cw)
# fit表示训练模型,batch_size表示每次训练的样本数,epochs表示训练的轮数,validation_split表示验证集的比例,verbose表示日志显示,0表示不显示
训练之后,画出accracy和loss随着训练次数的变化图。我们认为,接近1的正确率说明训练收敛情况良好。
plt.subplots(1,2,figsize = (9.0,4.5),sharex = True) # sharex表示共享x轴
plt.subplot(1,2,1)
plt.plot(hist.epoch,hist.history['accuracy'],\
color = 'black',lw = 2.50)
# hist.epoch表示训练的轮数,hist.history['accuracy']表示训练集的准确率,可以看到随着训练的轮数增加,训练集的准确率也在增加
plt.ylabel('1D-CNN Accuracy')
plt.xlabel('Epoch')
plt.subplot(1,2,2)
plt.plot(hist.epoch,hist.history['loss'],\
color = 'pink',lw = 2.50)
plt.ylabel('1D-CNN Loss')
plt.xlabel('Epoch')
plt.tight_layout()
plt.show()
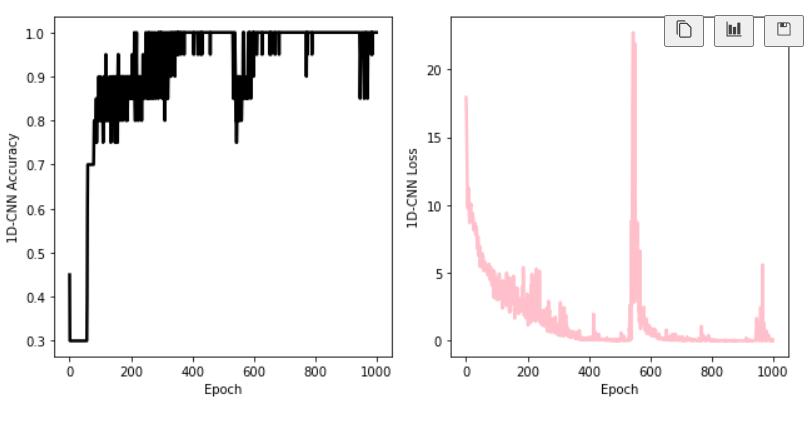
可以发现,模型的准确率高到90%。
评估模型的变现:
print(mdl.evaluate(Xtest,ytest,verbose = 2)) # evaluate表示评估模型
输出结果如下:
1/1 - 0s - loss: 0.4079 - accuracy: 0.9200 - 28ms/epoch - 28ms/step
[0.4079207181930542, 0.9200000166893005]
分类报告显示了每个类的精度、召回率和f1-score的详细信息,包括模型的整体性能。
# print(classification_report(np.where(ytest != 0)[1],\
# mdl.predict_classes(Xtest)))
predict=mdl.predict(Xtest)
classes_x=np.argmax(predict,axis=1)
print(classification_report(np.where(ytest != 0)[1],\
classes_x))
输出结果如下:
1/1 [==============================] - 0s 37ms/step
precision recall f1-score support
0 1.00 0.88 0.94 17
1 0.80 1.00 0.89 8
accuracy 0.92 25
macro avg 0.90 0.94 0.91 25
weighted avg 0.94 0.92 0.92 25
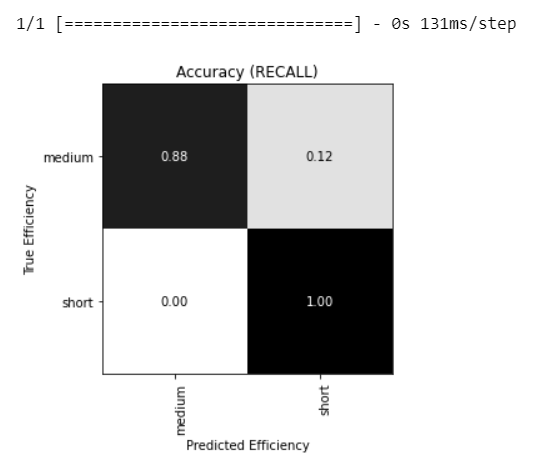
通过下面描述的混淆矩阵,可以更直观地显示召回率:
plotConfusionMatrix(np.argmax(ytest,axis = 1),\
np.argmax(mdl.predict(Xtest),axis = 1),\
['medium','short'],\
bsize = 1.75,cmap = 'binary')
plt.title('Accuracy (RECALL)')
plt.show()
附录
深度学习评价标准
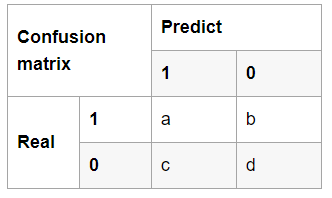
TP(a):实际正类预测为正类的数量;FN(b):实际正类预测为负类的数量
FP(c):实际负类预测为正类的数量;TN(d):实际负类预测为负类的数量
IoU交并比:用于判断检测出的目标是否和真值目标框匹配,即判断是tp、fp还是fn
\[IoU = tp/(tp+fp+fn)\]Precision 精确率(也就是查准率):
\[Precision = tp /(tp+fp)\]Recall召回率(也即是查全率)
\[Recall = tp/(tp+fn)\]P-R曲线
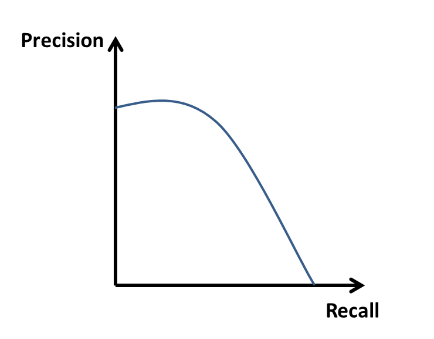
从图中可以看出,Precision高,Recall就很难做到非常高;Recall高,Precision就很难做到很高。因此,一般画出P-R曲线发现成反比例。于是,产生问题:
- 如何选取最合适的阈值以平衡Precision和Recall? 答案:可利用F1 score寻找Precision和Recall之间的最优平衡,即选择使得F1 score取得最大值时对应的阈值。
频谱峰度(Kurtosis Spectogram)
谱峭度(Spectrum kurtosis,SK)的概念最先由Dwyer在1983年提出,其本质是计算每根谱线峭度值的高阶统计量。谱峭度对信号中的瞬态冲击成分十分敏感,能有效的从含有背景噪声信号中识别瞬态冲击及其在频带中的分布。由于谱峭度的复杂性、缺少一个正式的定义和一个容易理解的计算过程使其在很长时间内都未能引入到工程应用中,直到Antoni等在2006年为谱峭度做了详细的定义,并提出了基于短时傅里叶变换的SK估计器,将理论概念与实际应用联系起来,提出了Kurtogram算法,并阐述了该算法在旋转机械故障特征提取领域的具体应用过程。
1D CNN
写不动了!!!





