插件下载地址
pycharm-文件-设置-插件-搜索ChatGPTplus:
prompt举例
插入排序算法,需要有及其详细的注释和print,并给出例子
冒泡排序算法
def bubble_sort(arr):
"""
冒泡排序算法
:param arr: 待排序的列表
:return: 排序后的列表
"""
n = len(arr)
# 遍历n-1次,每次将最大值移动到末尾
for i in range(n-1):
# 每次遍历比较相邻的两个元素
for j in range(n-i-1):
# 如果前一个元素大于后一个元素,则交换它们的位置
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
print(f"第{i+1}次遍历后的结果:{arr}")
return arr
if __name__ == '__main__':
arr = [3, 5, 4, 1, 2, 6]
print(f"排序前的列表:{arr}")
print(f"排序后的列表:{bubble_sort(arr)}")
结果如下:
排序前的列表:[3, 5, 4, 1, 2, 6]
第1次遍历后的结果:[3, 4, 1, 2, 5, 6]
第2次遍历后的结果:[3, 1, 2, 4, 5, 6]
第3次遍历后的结果:[1, 2, 3, 4, 5, 6]
第4次遍历后的结果:[1, 2, 3, 4, 5, 6]
第5次遍历后的结果:[1, 2, 3, 4, 5, 6]
排序后的列表:[1, 2, 3, 4, 5, 6]
二分法搜索算法
乱入了一个奇奇怪怪的东西
def binary_search(arr, target):
"""
二分法搜索算法
:param arr: 有序数组
:param target: 目标值
:return: 目标值的索引或者 None
"""
left = 0 # 左边界
right = len(arr) - 1 # 右边界
while left <= right:
mid = (left + right) // 2 # 取中间值
if arr[mid] == target: # 如果中间值等于目标值,返回索引
return mid
elif arr[mid] < target: # 如果中间值小于目标值,在右半部分寻找
left = mid + 1
else: # 如果中间值大于目标值,在左半部分寻找
right = mid - 1
return None # 没有找到目标值,返回 None
if __name__ == '__main__':
arr = [1, 2, 3, 4, 5, 6]
print(f"二分法搜索算法:{binary_search(arr, 5)}")
print(f"二分法搜索算法:{binary_search(arr, 7)}")
'''
假设我们要在一个有序数组中查找一个特定的元素,可以使用二分法算法。
二分法算法是一种高效的算法,通常用于在大型、有序数据集中查找特定的值。
算法的基本思想是将数组分成两部分,然后比较中间值和目标值。
如果中间值等于目标值,则返回中间值的索引。
如果中间值大于目标值,则在左半部分中查找。
如果中间值小于目标值,则在右半部分中查找。反复进行这个过程,直到找到目标值或者确定目标值不存在。
'''
结果如下:
二分法搜索算法:4
二分法搜索算法:None
选择排序算法
选择排序算法是一种简单直观的排序算法,它的基本思想是每次找到未排序部分中的最小元素,然后将其放到已排序部分的末尾。
接下来,我们用一个例子来演示选择排序算法的执行过程。
假设待排序数组为[64, 25, 12, 22, 11],则选择排序算法的执行过程如下:
首先,未排序部分包括整个数组,已排序部分为空。
第一次循环,找到未排序部分的最小元素11,将其与已排序部分的末尾交换位置,得到[11, 25, 12, 22, 64]。此时已排序部分包括元素11。
第二次循环,找到未排序部分的最小元素12,将其与已排序部分的末尾交换位置,得到[11, 12, 25, 22, 64]。此时已排序部分包括元素11和12。
第三次循环,找到未排序部分的最小元素22,将其与已排序部分的末尾交换位置,得到[11, 12, 22, 25, 64]。此时已排序部分包括元素11、12和22。
第四次循环,找到未排序部分的最小元素25,将其与已排序部分的末尾交换位置,得到[11, 12, 22, 25, 64]。此时已排序部分包括元素11、12、22和25。
最后,未排序部分为空,排序完成。
def selection_sort(arr):
n = len(arr)
for i in range(n):
# 找到未排序部分的最小元素
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
# 将最小元素放到已排序部分的末尾
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# 打印每次交换后的数组
print(arr)
# 示例
arr = [64, 25, 12, 22, 11]
selection_sort(arr)
print("排序后的数组:", arr)
输出结果如下:
[11, 25, 12, 22, 64]
[11, 12, 25, 22, 64]
[11, 12, 22, 25, 64]
[11, 12, 22, 25, 64]
[11, 12, 22, 25, 64]
排序后的数组: [11, 12, 22, 25, 64]
插入排序
插入排序算法的基本思想是将未排序的元素插入到已排序的元素中,从而得到一个有序的序列。具体实现方式是,先将第一个元素视为已排序的序列,然后逐个将未排序的元素插入到已排序的序列中,直到所有元素都被插入。
def insertion_sort(arr):
# 遍历整个数组
for i in range(1, len(arr)):
# 将待排序元素存储在临时变量中
temp = arr[i]
j = i - 1
# 将已排序元素中比待排序元素大的元素向右移动
while j >= 0 and arr[j] > temp:
arr[j + 1] = arr[j]
j -= 1
# 将待排序元素插入到正确位置
arr[j + 1] = temp
# 打印每次排序后的数组
print(arr)
return arr
# 示例
arr = [3,1,4,5,2]
print(f"排序前的列表:{arr}")
print(f"排序后的列表:{insertion_sort(arr)}")
输出结果如下:
排序前的列表:[3, 1, 4, 5, 2]
[1, 3, 4, 5, 2]
[1, 3, 4, 5, 2]
[1, 3, 4, 5, 2]
[1, 2, 3, 4, 5]
排序后的列表:[1, 2, 3, 4, 5]
希尔排序
希尔排序是一种插入排序的改进算法,也称为缩小增量排序。它通过将待排序的数组分割成几个子数组来提高插入排序的性能,每个子数组使用插入排序进行排序,最后再合并为完整的有序数组。
def shell_sort(arr):
# 计算数组 arr 的长度 n
n = len(arr)
# 计算初始的增量 gap,通常设置为 n 的一半
gap = n // 2
# 进入一个 while 循环,当 gap 大于 0 时,执行以下操作
while gap > 0:
# 从 gap 开始,对数组 arr 进行插入排序,
#具体实现是从 i = gap 开始,依次将 arr[i] 插入到 arr[0] 到 arr[i-gap] 的位置上,这里的 arr[0] 到 arr[i-gap] 就是一个子序列
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
# 每次插入排序结束后,将 gap 除以 2,继续进行下一轮排序
gap //= 2
return arr
if __name__ == 'main':
arr = [64, 34, 25, 12, 22, 11, 90]
print("Original array:", arr)
sorted_arr = shell_sort(arr)
print("Sorted array:", sorted_arr)
在这个实现中,我们使用了一个变量 gap来表示子序列的间隔大小。开始时,gap的大小为序列长度的一半。然后,在每次循环中,我们将 gap的大小减半,直到 gap等于1。
在每次循环中,我们对每个子序列进行插入排序。具体来说,对于第 i个子序列,我们将它的第 gap个元素作为起点,然后将它后面每个 gap个元素与前面已经排好序的子序列进行比较,插入到正确的位置。
在这个例子中,我们将待排序的数组分割成2个子数组,分别为[64, 25, 22, 90]和[34, 12, 11]。然后对每个子数组进行插入排序,最后将它们合并为一个完整的有序数组。
输出结果如下:
Original array: [64, 34, 25, 12, 22, 11, 90]
Sorted array: [11, 12, 22, 25, 34, 64, 90]
下期预告
归并排序
堆排序
计数排序
桶排序
基数排序
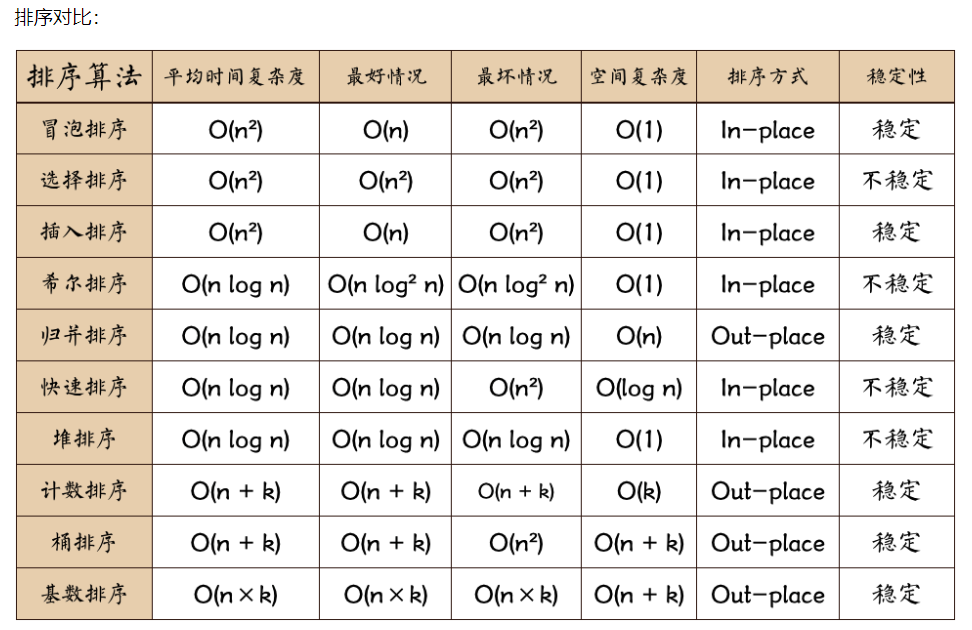
对比