深度学习与图像处理（七）- Pytorch基础和手写数字识别实战

2023-05-27 | 阅读：次

机器学习工作流

(1) 定义问题：有哪些数据可用？你想要预测什么？你是否需要收集更多数据或雇人为数据集手动添加标签？ (2) 找到能够可靠评估目标成功的方法。对于简单任务，可以用预测精度，但很多情况都需要与领域相关的复杂指标。 (3) 准备用于评估模型的验证过程。训练集、验证集和测试集是必须定义的。验证集和测试集的标签不应该泄漏到训练数据中。举个例子，对于时序预测，验证数据和测试数据的时间都应该在训练数据之后。 (4) 数据向量化。方法是将数据转换为向量并预处理，使其更容易被神经网络所处理（数据标准化等）。 (5) 开发第一个模型，它要打败基于常识的简单基准方法，从而表明机器学习能够解决你的问题。事实上并非总是如此！ (6) 通过调节超参数和添加正则化来逐步改进模型架构。仅根据模型在验证集（不是测试集或训练集）上的性能来进行更改。请记住，你应该先让模型过拟合（从而找到比你的需求更大的模型容量），然后才开始添加正则化或降低模型尺寸。 (7) 调节超参数时要小心验证集过拟合，即超参数可能会过于针对验证集而优化。我们保留一个单独的测试集，正是为了避免这个问题。

Pytorch基础

GPU和CPU

GPU（Graphics Processing Unit）又被称作图像处理器，是一台主机的显示处理核心，主要负责对计算机中的图形和图像的处理与运算。它们之间的具体差异如下。（1）核心数：GPU 相较于 CPU 的硬件构成，在结构上拥有更多的核心数量，虽然 GPU的核心数量更多，但是 CPU 中的单个核心相对于 GPU 中的单个核心，拥有更快速、高效的算力。（2）应用场景：在应用场景上 GPU 和 CPU 也各有侧重，GPU 适用于需要并行计算能力的场景，比如图像处理；CPU 更适用于需要串行计算能力的场景，比如计算机的指令处理。

CPU 都是为了计算而生的，那么我们为什么还会强力推荐将 GPU作为核心算力的输出硬件呢？这是因为在深度学习模型中生成的参数结构都是张量（Tensor）形式的，矩阵和张量的算术运算的模式就是一种并行运算。所以张量的算术运算在 GPU 的加持下会获得比 CPU 更快速、高效的计算能力，因此在对深度学习参数的训练和优化过程中，GPU 能够为我们提供更多的帮助。

import time 
import torch 
for i in range(1,10): 
    start = time.time() 
    a = torch.FloatTensor(i*100,1000,1000) 
    a = torch.matmul(a,a) 
    end = time.time()-start 
    print(end)

torch.FloatTensor()函数用于生成张量，torch.matmul()函数用于矩阵乘法运算，time.time()函数用于获取当前时间戳，end-start用于计算时间差。

在这里，张量的维度从(100,1000,1000)到(1000,1000,1000)逐次累加，所需要的运算耗时如下：

1.6489999294281006
2.9369986057281494
4.34499979019165
5.8696980476379395
7.847997665405273
8.423005104064941
9.7409987449646
12.301092147827148
14.527003526687622

以上代码加上GPU加速(a=a.cuda())后的运行时间几乎不会有变化，说明GPU 的并行计算能力很强。

检测是否支持GPU：

import torch
print(torch.cuda.is_available())
print(torch.__version__)

张量Tensor

张量是一个多维数组，它是一个标量、向量、矩阵的泛化。PyTorch中的张量和numpy中的array很类似。

函数名	数据类型
torch.FloatTensor	浮点型Tensor
torch.IntTensor	整型Tensor
torch.rand	生成在0-1之间均匀分布的指定维度的随机Tensor
torch.randn	随机生成均值为0，方差为1的正太分布
torch.range(start,range,step)
torch.zeros

tensor中的运算

torch.clamp(input, min, max, out=None)

将输入input张量每个元素的夹紧到区间 [min,max]，并返回结果到一个新张量。(元素小于裁剪范围时，取min；大于裁剪范围时，取max)

自动梯度

实现自动梯度功能的过程大致为：先通过输入的 Tensor 数据类型的变量在神经网络的前向传播过程中生成一张计算图，然后根据这个计算图和输出结果准确计算出每个参数需要更新的梯度，最后通过完成后向传播完成对参数的梯度更新。

在实践中完成自动梯度需要用到 torch.autograd 包中的 Variable 类对我们定义的 Tensor 数据类型变量进行封装，在封装后，计算图中的各个节点就是一个 Variable 对象，这样才能应用自动梯度的功能。

用X代表我们选中的节点，X.grad是一个Variable对象，不过它表示的是X的梯度，在访问梯度时候要使用X.grad.data。

# import time 
# import torch 
# for i in range(1,10): 
#     start = time.time() 
#     a = torch.FloatTensor(i*100,1000,1000) 
#     a = torch.matmul(a,a) 
#     end = time.time()-start 
#     print(end) 


import torch
from torch.autograd import Variable
batch_n = 100
hidden_layer = 100
input_data = 1000
output_data = 10

x = Variable(torch.randn(batch_n,input_data),requires_grad=False)
y = Variable(torch.randn(batch_n,output_data),requires_grad=False)

w1 = Variable(torch.randn(input_data,hidden_layer),requires_grad=True)
w2 = Variable(torch.randn(hidden_layer,output_data),requires_grad=True)

# 训练次数和学习率
epoch_n = 20 
learning_rate = 1e-6

# 模型训练和参数更新
for epoch in range(epoch_n):
    y_pred = x.mm(w1).clamp(min=0).mm(w2) 
    # mm表示矩阵乘法，
    #clamp表示夹紧，相当于激活函数
    loss = (y_pred - y).pow(2).sum() 
    print("Epoch:{},Loss:{:.4f}".format(epoch,loss.item()))
    # loss.data是一个标量张量，它没有维度，因此不能使用loss.data[0]来访问它的值。
  
    loss.backward()

    # 更新参数
    w1.data -= learning_rate * w1.grad.data
    w2.data -= learning_rate * w2.grad.data

    w1.grad.data.zero_() # 梯度清零
    w2.grad.data.zero_() # 梯度清零

这段代码中，使用Variable类对Tensor数据类型进行了封装，requires_grad参数为False时候，变量在自动梯度计算的过程中不会保留梯度值。对于输入的x和输出的y，不需要保留梯度值；但是对于两个权重w1和w2,需要设置为True保留参数。

在代码的最后还要将本次计算得到的各个参数节点的梯度值通过 grad.data.zero_()全部置零，如果不置零，则计算的梯度值会被一直累加，这样就会影响到后续的计算。

输出结果如下：

Epoch:0,Loss:42458792.0000
Epoch:1,Loss:80534832.0000
Epoch:2,Loss:333504672.0000
Epoch:3,Loss:851591680.0000
Epoch:4,Loss:112547912.0000
Epoch:5,Loss:26212034.0000
Epoch:6,Loss:14902239.0000
Epoch:7,Loss:9971557.0000
Epoch:8,Loss:7236613.0000
Epoch:9,Loss:5534734.0000
Epoch:10,Loss:4387320.0000
Epoch:11,Loss:3568915.2500
Epoch:12,Loss:2962310.7500
Epoch:13,Loss:2497898.7500
Epoch:14,Loss:2133571.2500
Epoch:15,Loss:1841966.7500
Epoch:16,Loss:1605802.0000
Epoch:17,Loss:1411681.5000
Epoch:18,Loss:1250214.2500
Epoch:19,Loss:1114617.1250

除了采用自动梯度的方法，我们还可以通过构建一个继承了torch.mm.Module类的类来实现神经网络的前向传播和后向传播，这种方法更加灵活，可以自定义神经网络的结构。

下面介绍如何使用自定义传播函数的方法，来调整之前具备自动梯度功能的简易神经网络模型。

import torch
from torch.autograd import Variable
batch_n = 100
hidden_layer = 100
input_data = 1000
output_data = 10

x = Variable(torch.randn(batch_n,input_data),requires_grad=False)
y = Variable(torch.randn(batch_n,output_data),requires_grad=False)

w1 = Variable(torch.randn(input_data,hidden_layer),requires_grad=True)
w2 = Variable(torch.randn(hidden_layer,output_data),requires_grad=True)

# 训练次数和学习率
epoch_n = 20 
learning_rate = 1e-6

class Model(torch.nn.Module):
    def __init__(self):
        super(Model,self).__init__()
    def forward(self,input,w1,w2):
        x = torch.mm(input,w1)
        x = torch.clamp(x,min=0)
        x = torch.mm(x,w2)
        return x
    def backward(self):
        pass

# 模型训练和参数更新
model = Model()

for epoch in range(epoch_n):
    y_pred = model(x,w1,w2)
    loss = (y_pred - y).pow(2).sum()
    print("Epoch:{},Loss:{:.4f}".format(epoch,loss.item()))

    # 更新参数
    loss.backward()
    w1.data -= learning_rate * w1.grad.data
    w2.data -= learning_rate * w2.grad.data

    w1.grad.data.zero_() # 梯度清零
    w2.grad.data.zero_() # 梯度清零

以上代码展示了一个比较常用的 Python 类的构造方式：首先通过 class Model(torch.nn. Module)完成了类继承的操作，之后分别是类的初始化，以及 forward 函数和 backward 函数。forward 函数实现了模型的前向传播中的矩阵运算，backward 实现了模型的后向传播中的自动梯度计算，后向传播如果没有特别的需求，则在一般情况下不用进行调整。在定义好类之后，我们就可以对其进行调用了(model = Model())，代码如下

模型搭建和优化

PyTorch 中已定义的类和方法覆盖了神经网络中的线性变换、激活函数、卷积层、全连接层、池化层等常用神经网络结构的实现。

torcn.nn

下面是使用Pytorch中的torch.nn简化之前的代码，这里仅仅定义了4个变量，分别是输入层的神经元个数、隐藏层的神经元个数、输出层的神经元个数和训练次数。但是这里仅仅定义了输入和输出的变量，之前代码中的权重w1和w2都没有定义，这是因为在torch.nn中，我们可以自动生成和初始化对应维度的权重参数。

import torch
from torch.autograd import Variable
batch_n = 100
hidden_layer = 100
input_data = 1000
output_data = 10

x = Variable(torch.randn(batch_n,input_data),requires_grad=False)
y = Variable(torch.randn(batch_n,output_data),requires_grad=False)

# 使用torch.nn搭建模型

models = torch.nn.Sequential(
    torch.nn.Linear(input_data,hidden_layer),
    torch.nn.ReLU(),
    torch.nn.Linear(hidden_layer,output_data)
)

torch.nn.Sequential 括号内的内容就是我们搭建的神经网络模型的具体结构，这里首先通过 torch.nn.Linear(input_data, hidden_layer)完成从输入层到隐藏层的线性变换，然后经过激活函数及 torch.nn.Linear(hidden_layer, output_data)完成从隐藏层到输出层的线性变换。

torch.nn.Sequential 类是 torch.nn 中的一种序列容器，可以嵌套套各种实现神经网络中具体功能相关的类，来完成对神经网络模型的搭建，我们可以将嵌套在容器中的各个部分看作各种不同的模块，这些模块可以自由组合。模块的加入一般有两种方式，一种是在以上代码中使用的直接嵌套，另一种是以 orderdict 有序字典的方式进行传入，这两种方式的唯一区别是，使用后者搭建的模型的每个模块都有我们自定义的名字，而前者默认使用从零开始的数字序列作为每个模块的名字。

两者的区别如下所示：

hidden_layer = 100 
input_data = 1000 
output_data = 10 
models = torch.nn.Sequential( 
    torch.nn.Linear(input_data, hidden_layer), 
    torch.nn.ReLU(), 
    torch.nn.Linear(hidden_layer, output_data) 
) 
print(models)

输出结果如下：

Sequential(
  (0): Linear(in_features=1000, out_features=100, bias=True)
  (1): ReLU()
  (2): Linear(in_features=100, out_features=10, bias=True)
)

使用orderdict的方式：

hidden_layer = 100
input_data = 1000
output_data = 10

from collections import OrderedDict
models = torch.nn.Sequential(OrderedDict([
    ('linear1',torch.nn.Linear(input_data,hidden_layer)),
    ('relu',torch.nn.ReLU()),
    ('linear2',torch.nn.Linear(hidden_layer,output_data))
]))
print(models)

输出结果如下：

Sequential(
  (linear1): Linear(in_features=1000, out_features=100, bias=True)
  (relu): ReLU()
  (linear2): Linear(in_features=100, out_features=10, bias=True)
)

下面简单对已经搭建好的模型进行训练和优化参数：

epoch_n = 10000
learning_rate = 1e-4
loss_fn = torch.nn.MSELoss() # 用在torch.nn中已经定义好的均方误差函数类来计算损失值

for epoch in range(epoch_n):
    y_pred = models(x)
    loss = loss_fn(y_pred,y)
    # % 1000 == 0 每隔1000次输出一次
    if epoch % 1000 == 0:
        print("Epoch:{},Loss:{:.4f}".format(epoch,loss.item()))
    models.zero_grad() # 梯度清零
    loss.backward() # 反向传播
    for param in models.parameters():
        param.data -= param.grad.data * learning_rate

可以看出，参数的优化效果比较理想，loss 值被控制在相对较小的范围之内:

Epoch:0,Loss:1.0804
Epoch:1000,Loss:0.9975
Epoch:2000,Loss:0.9263
Epoch:3000,Loss:0.8641
Epoch:4000,Loss:0.8089
Epoch:5000,Loss:0.7592
Epoch:6000,Loss:0.7139
Epoch:7000,Loss:0.6724
Epoch:8000,Loss:0.6343
Epoch:9000,Loss:0.5989

torch.optim

到目前为止，代码中的神经网络权重的参数优化和更新还没有实现自动化，并且目前使用的优化方法都有固定的学习速率，所以优化函数相对简单，如果我们自己实现一些高级的参数优化算法，则优化函数部分的代码会变得较为复杂。在 PyTorch 的 torch.optim 包中提供了非常多的可实现参数自动优化的类，比如 SGD、AdaGrad、RMSProp、Adam 等，这些类都可以被直接调用，使用起来也非常方便。

下面我们使用 torch.optim 中的Adam 类来实现对神经网络模型的参数优化：

import torch
from torch.autograd import Variable
batch_n = 100
hidden_layer = 100
input_data = 1000
output_data = 10

x = Variable(torch.randn(batch_n,input_data),requires_grad=False)
y = Variable(torch.randn(batch_n,output_data),requires_grad=False)

# 使用torch.nn搭建模型
models = torch.nn.Sequential(
    torch.nn.Linear(input_data,hidden_layer),
    torch.nn.ReLU(),
    torch.nn.Linear(hidden_layer,output_data)
)

epoch_n = 100
learning_rate = 1e-4
loss_fn = torch.nn.MSELoss() # 用在torch.nn中已经定义好的均方误差函数类来计算

# 模型优化
optimizer = torch.optim.Adam(models.parameters(),lr=learning_rate)

for epoch in range(epoch_n):
    y_pred = models(x)
    loss = loss_fn(y_pred,y)

    if epoch % 10 == 0:
        print("Epoch:{},Loss:{:.4f}".format(epoch,loss.item()))

    optimizer.zero_grad() # 梯度清零
    loss.backward() # 反向传播
    optimizer.step() # 更新参数

这里使用了 torch.optim 包中的 torch.optim.Adam 类作为我们的模型参数的优化函数，在 torch.optim.Adam 类中输入的是被优化的参数和学习速率的初始值，如果没有输入学习速率的初始值，那么默认使用 0.001 这个值。因为我们需要优化的是模型中的全部参数，所以传递给 torch.optim.Adam 类的参数是 models.parameters。另外，Adam 优化函数可以对梯度更新使用到的学习速率进行自适应调节。

输出结果如下：

Epoch:0,Loss:1.1064
Epoch:10,Loss:0.8949
Epoch:20,Loss:0.7313
Epoch:30,Loss:0.5999
Epoch:40,Loss:0.4939
Epoch:50,Loss:0.4058
Epoch:60,Loss:0.3311
Epoch:70,Loss:0.2681
Epoch:80,Loss:0.2155
Epoch:90,Loss:0.1714

可以发现，仅仅使用了 100 次迭代，loss 值就已经降到了 0.17 左右，远低于之前进行10000次优化训练的结果，说明torch.optim效果非常理想。

手写数字识别实战

torchvision 包的主要功能是实现数据的处理、导入和预览等，所以如果需要对计算机视觉的相关问题进行处理，就可以借用在 torchvision 包中提供的大量的类来完成相应的工作。

其中，root 用于指定数据集在下载之后的存放路径，这里存放在根目录下的 data 文件夹中；transform 用于指定导入数据集时需要对数据进行哪种变换操作，；train 用于指定在数据集下载完成后需要载入哪部分数据，如果设置为 True，则说明载入的是该数据集的训练集部分；如果设置为 False，则说明载入的是该数据集的测试集部分。

import torch 
from torchvision import transforms,datasets
from torch.autograd import Variable # 用于将tensor转换成Variable来进行梯度计算


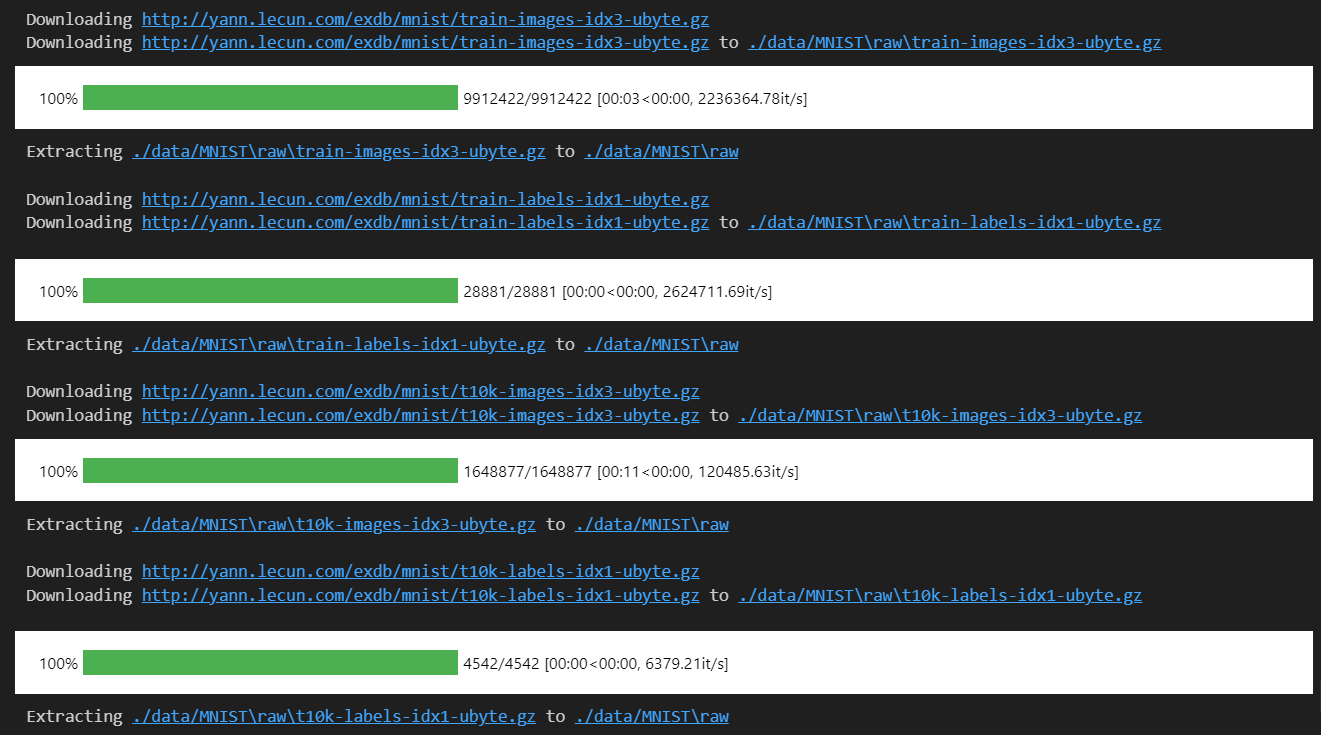
# 下载训练集 MNIST 手写数字训练集
data_train = datasets.MNIST(root="./data/",
                            transform=transforms.ToTensor(),
                            train=True,
                            download=True)
data_test = datasets.MNIST(root="./data/",
                            transform=transforms.ToTensor(),
                            train=False)

20230527112128

数据增强data argumentation

torch.transforms 中提供了丰富的类对载入的数据进行变换，比如说对图像进行旋转、裁剪、缩放、翻转等操作，这些操作可以增加数据集的多样性，从而提高模型的泛化能力。

函数名称	功能
torchvision.transforms.Resize	按照需求大小进行缩放，比如说传入一个类似于(h,w)的序列，或者一个整数型数据)
torchvision.transforms.ToTensor	对载入的图像数据进行类型转换，比如说PIL图片的数据转换成Tensor数据类型的变量
torchvision.transforms.RandomVerticalFlip	对输入图片按照随机概论水平翻转，默认的概率为0.5

transform=transform.Compose([transforms.ToTensor(),
                            transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])

在 torchvision.transforms.Compose 中只使用了一个类型的转换变换transforms.ToTensor 和一个数据标准化变换 transforms.Normalize,标准化的计算公式如下：

\[X^{normal} = \frac{X-mean}{std}\]

数据预览和装载

在数据下载完成并且载入后，我们还需要对数据进行装载。我们可以将数据的载入理解为对图片的处理，在处理完成后，我们就需要将这些图片打包好送给我们的模型进行训练了，而装载就是这个打包的过程。在装载时通过 batch_size 的值来确认每个包的大小，通过 shuffle 的值来确认是否在装载的过程中打乱图片的顺序。

# 数据装载
data_loader_train = torch.utils.data.DataLoader(dataset=data_train,
                                                batch_size=64,
                                                shuffle=True)

data_loader_test = torch.utils.data.DataLoader(dataset=data_test,
                                                batch_size=64,
                                                shuffle=True)

对数据的装载使用的是 torch.utils.data.DataLoader 类，类中的 dataset 参数用于指定我们载入的数据集名称，batch_size 参数设置了每个包中的图片数据个数，代码中的值是 64，所以在每个包中会包含 64 张图片。将 shuffle 参数设置为 True，在装载的过程会将数据随机打乱顺序并进行打包。

对数据进行预览如下：

# 数据预览
images, labels = next(iter(data_loader_train)) 
# iter()生成迭代器，next()返回迭代器的下一个项目

img = torchvision.utils.make_grid(images)
img = img.numpy().transpose(1,2,0)
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean
print([labels[i] for i in range(64)])
plt.imshow(img)

传递给utils.make_grid的参数是一个批次的数据，即64张图片，每个批次的装载数据都是4维的，即[64,1,28,28]，其中64表示批次大小，1表示通道数，28表示图片的高度，28表示图片的宽度。而make_grid函数的作用是将批次的图片数据拼接成一张图片。得到的img维度变成(channel,height,width)，即[3,242,242]，其中3表示通道数，242表示图片的高度，242表示图片的宽度。

transpose对img进行转置并转换为numpy数组，即[242,242,3]，这是因为想使用 Matplotlib 将数据显示成正常的图片形式，则使用的数据首先必须是数组，其次这个数组的维度必须是（height,weight,channel）。

输出结果如下：

[tensor(2), tensor(8), tensor(8), tensor(9), tensor(4), tensor(1), tensor(1), tensor(3), tensor(0), tensor(0), tensor(9), tensor(7), tensor(7), tensor(4), tensor(6), tensor(7), tensor(7), tensor(5), tensor(4), tensor(1), tensor(8), tensor(3), tensor(4), tensor(2), tensor(6), tensor(0), tensor(2), tensor(4), tensor(4), tensor(6), tensor(6), tensor(1), tensor(8), tensor(0), tensor(9), tensor(9), tensor(2), tensor(2), tensor(0), tensor(4), tensor(7), tensor(5), tensor(8), tensor(7), tensor(0), tensor(9), tensor(8), tensor(2), tensor(2), tensor(8), tensor(8), tensor(5), tensor(8), tensor(0), tensor(2), tensor(3), tensor(7), tensor(8), tensor(1), tensor(8), tensor(2), tensor(4), tensor(3), tensor(9)]

20230527115022

模型搭建和参数优化

我们想要搭建一个包含了卷积层、激活函数、池化层、全连接层的卷积神经网络来解决这个问题。而这些可以通过torch.nn来实现，卷积层用torch.nn.Conv2d来实现，激活函数用torch.nn.ReLU来实现，最大池化层用torch.nn.MaxPool2d来实现，全连接层用torch.nn.Linear来实现。

# 模型搭建和参数优化
class Model(torch.nn.Module):
    def __init__(self):
        super(Model,self).__init__() # 调用父类的初始化函数，即先运行nn.Module的初始化函数
        self.conv1 = torch.nn.Sequential(
            torch.nn.Conv2d(1,64,kernel_size=3,stride=1,padding=1),
            torch.nn.ReLU(),
            torch.nn.Conv2d(64,128,kernel_size=3,stride=1,padding=1),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(stride=2,kernel_size=2))
  
        self.dense = torch.nn.Sequential(
            torch.nn.Linear(14*14*128,1024),
            torch.nn.ReLU(),
            torch.nn.Dropout(p=0.5),
            torch.nn.Linear(1024,10))
  
    def forward(self,x):
        x = self.conv1(x)
        x = x.view(-1,14*14*128)
        x = self.dense(x)
        return x

torch.nn.Conv2d：用于搭建卷积神经网络的卷积层，主要的输入参数有输入通道数、输出通道数、卷积核大小、卷积核移动步长和 Paddingde 值。在这个简化的模型中，用了两个卷积层，第一个卷积层的输入通道数为 1，输出通道数为 64，卷积核大小为 3，卷积核移动步长为 1，Padding 值为 1。第二个卷积层的输入通道数为 64，输出通道数为 128，卷积核大小为 3，卷积核移动步长为 1，Padding 值为 1。

如何知道输入和输出通道数量？

输出数据的通道数是由卷积核的数量决定的。卷积核的数量就是输出通道数 $C_{out}$，每个卷积核对应输出数据的一个通道。在训练过程中，每个卷积核会学习一组权重参数，用于提取输入数据的不同特征。因此，卷积层的输出通道数（即卷积核的数量）通常是作为网络的一个超参数来设定的，需要根据具体的任务和网络结构进行调整。

设输入数据的高度和宽度分别为 $H_{in}$ 和 $W_{in}$，卷积核的高度和宽度分别为 $H_k$ 和 $W_k$，步长为 $S$，填充大小为 $P$，则输出数据的高度和宽度分别为：

\[H_{out} = \lfloor \frac{H_{in} + 2P - H_k}{S} \rfloor + 1\] \[W_{out} = \lfloor \frac{W_{in} + 2P - W_k}{S} \rfloor + 1\]

torch.nn.ReLU: 用于搭建激活函数。

torch.nn.MaxPool2d: 用于搭建最大池化层，主要的输入参数有池化核大小和池化核移动步长(stride=2表示池化核移动步长为2)。

最大池化操作之后，输出数据的高度和宽度分别为：

\[H_{out} = \lfloor \frac{H_{in} - H_k}{S} \rfloor + 1\] \[W_{out} = \lfloor \frac{W_{in} - W_k}{S} \rfloor + 1\]

self.dense表示全连接层，输入的数据是二维的，即[batch_size,14*14*128]，输出的数据是一维的，即[batch_size,10]。这里的14*14*128是通过计算得到的，具体的计算过程如下：

第一个卷积层的输出数据的高度和宽度分别为：

\[H_{out} = \lfloor \frac{H_{in} + 2P - H_k}{S} \rfloor + 1 = \lfloor \frac{28 + 2 - 3}{1} \rfloor + 1 = 28\] \[W_{out} = \lfloor \frac{W_{in} + 2P - W_k}{S} \rfloor + 1 = \lfloor \frac{28 + 2 - 3}{1} \rfloor + 1 = 28\]

第二个卷积层的输出数据的高度和宽度分别为：

再经过一次最大池化操作之后，输出数据的高度和宽度分别为：

\[H_{out} = \lfloor \frac{H_{in} - H_k}{S} \rfloor + 1 = \lfloor \frac{28 - 2}{2} \rfloor + 1 = 14\] \[W_{out} = \lfloor \frac{W_{in} - W_k}{S} \rfloor + 1 = \lfloor \frac{28 - 2}{2} \rfloor + 1 = 14\]

torch.nn.Linear: 用于搭建全连接层，主要的输入参数有输入特征数量和输出特征数量。在这个简化的模型中，用了两个全连接层，第一个全连接层的输入特征数量为 14*14*128，输出特征数量为 1024。第二个全连接层的输入特征数量为 1024，输出特征数量为 10。

全连接层的输出数据维度是由全连接层的神经元数量决定的。假设输入数据的维度为 $(N, C_{in})$，其中 $N$ 表示 batch size，$C_{in}$ 表示输入特征的数量。全连接层的神经元数量为 $C_{out}$，则全连接层的输出数据维度为 $(N, C_{out})$。

全连接层的运算过程可以看做是一个矩阵乘法加上偏置的操作。具体来说，全连接层的每个神经元都与输入数据的每个特征相连，它所对应的权重参数构成了一个大小为 $(C_{in}, 1)$ 的列向量。将所有神经元的权重参数按列组合起来，就可以得到一个大小为 $(C_{in}, C_{out})$ 的权重矩阵 $W$。然后，将输入数据 $X$ 与权重矩阵 $W$ 相乘，得到一个大小为 $(N, C_{out})$ 的输出矩阵 $Y$。最后，再将每个神经元的偏置参数加到对应的输出上，得到最终的输出数据。

需要注意的是，在深度学习中，全连接层通常用于将卷积层或者池化层的输出特征图展平为一个向量，并将其输入到后续的全连接层中。因此，在实际应用中，全连接层的神经元数量通常是根据前面卷积层或者池化层输出数据的维度来设定的。如果输入数据的维度较大，全连接层的神经元数量也会相应增加，以保证网络的表达能力。

torch.nn.Dropout类是为了防止训练的模型对各部分的权重参数产生依赖导致过拟合，随机丢弃神经元（参数归零），下图是对于这一过程的示意图：

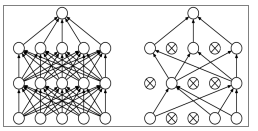
20230527143550

前向传播forwardd 函数中的内容。首先，经过 self.conv1 进行卷积处理；然后进行 x.view(−1, 1414128)，对参数实现扁平化，因为之后紧接着的就是全连接层，所以如果不进行扁平化，则全连接层的实际输出的参数维度和其定义输入的维度将不匹配，程序会报错；最后，通过 self.dense 定义的全连接进行最后的分类。

模型训练和优化

# 模型训练和优化

model = Model()
cost = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters())
print(model)

n_epochs = 5
for epoch in range(n_epochs):
    running_loss = 0.0 # 定义一个变量方便我们对loss进行输出
    running_correct = 0 # 定义一个变量方便我们计算预测对的数据个数，因为不是所有的预测都是100%正确的
    print("Epoch {}/{}".format(epoch,n_epochs))
    print("-"*10) # 用来分隔开输出结果
    for data in data_loader_train:
        X_train,y_train = data 
        X_train,y_train = Variable(X_train),Variable(y_train) 
        # 将tensor转换成Variable，因为只有Variable才具有梯度
    
        outputs = model(X_train) 
        _,pred = torch.max(outputs.data,1) # 找出每一行中最大值的下标，这是预测的分类结果

        optimizer.zero_grad() 
        # 由于loss.backward()的梯度是累加的，所以每次运算完一个batch后记得清空梯度

        loss = cost(outputs,y_train) # 计算损失值，注意传入的值是模型的输出值，而不是预测值

        loss.backward() # loss进行反向传播，根据参数的梯度

        optimizer.step() # 用来调整参数

        running_loss += loss.data.item() # loss本身为Variable类型，所以要使用data获取其Tensor，因为其为标量，所以取0

        running_correct += torch.sum(pred == y_train.data) # 计算预测对的数据个数
    testing_correct = 0 # 测试集中的预测正确的数量

    for data in data_loader_test:
        X_test,y_test = data
        X_test,y_test = Variable(X_test),Variable(y_test)
        outputs = model(X_test)
        _,pred = torch.max(outputs.data,1)
        testing_correct += torch.sum(pred == y_test.data)
    print("Loss is:{:.4f},Train Accuracy is:{:.4f}%,Test Accuracy is:{:.4f}"
          .format(running_loss/len(data_train),100*running_correct/len(data_train),100*testing_correct/len(data_test)))

训练输出结果如下：

Model(
  (conv1): Sequential(
    (0): Conv2d(1, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (3): ReLU()
    (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (dense): Sequential(
    (0): Linear(in_features=25088, out_features=1024, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=1024, out_features=10, bias=True)
  )
)
Epoch 0/5
----------
Loss is:0.0023,Train Accuracy is:95.5283%,Test Accuracy is:98.3200
Epoch 1/5
----------
Loss is:0.0008,Train Accuracy is:98.4700%,Test Accuracy is:98.5600
Epoch 2/5
----------
Loss is:0.0005,Train Accuracy is:98.9300%,Test Accuracy is:98.2000
Epoch 3/5
----------
Loss is:0.0004,Train Accuracy is:99.2467%,Test Accuracy is:98.7800
Epoch 4/5
----------
Loss is:0.0003,Train Accuracy is:99.3900%,Test Accuracy is:98.8200

随机验证

为了验证我们训练的模型是不是真的已如结果显示的一样准确，则最好的方法就是随机选取一部分测试集中的图片，用训练好的模型进行预测，看看和真实值有多大的偏差。


data_loader_test = torch.utils.data.DataLoader(dataset=data_test,batch_size=4,shuffle=True) # 一次4张图片

X_test,y_test = next(iter(data_loader_test)) # 读取一个batch的图片
inputs = Variable(X_test)
pred = model(inputs)
_,pred = torch.max(pred,1) # 找到概率最大的下标

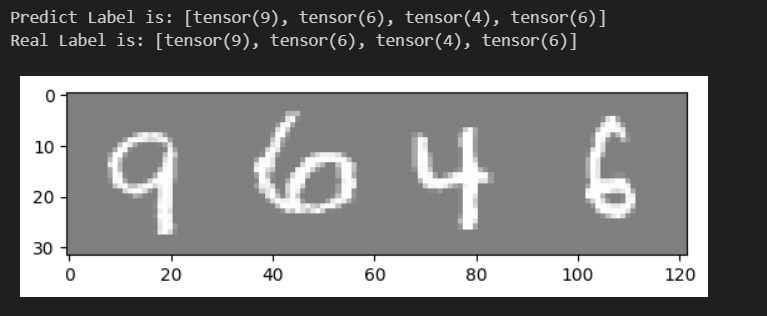
print("Predict Label is:",[i for i in pred.data])
print("Real Label is:",[i for i in y_test])

img = torchvision.utils.make_grid(X_test) # 把图片拼成一个图
img = img.numpy().transpose(1,2,0) # 把channel那一维放到最后
std = [0.5,0.5,0.5]
mean = [0.5,0.5,0.5]
img = img*std+mean # 去标准化
plt.imshow(img)
plt.show()

输出结果如下：

20230527153946

保存模型

# 保存网络的参数
torch.save(model.state_dict(),'./model/model.pth')
# 加载网络的参数
# 首先定义模型
model = Model()
model.load_state_dict(torch.load('./model/model.pth'))

# 保存整个网络
torch.save(model,'./model/model.pth')
# 加载整个网络
model = torch.load('./model/model.pth')

pth是模型的参数文件，保存的是模型的参数，不包含模型的结构。

如果还想保存某一次训练采用的优化器、epochs等信息，可将这些信息组合起来构成一个字典，然后将字典保存起来：

state = {'model': model.state_dict(), 'optimizer': optimizer.state_dict(), 'epoch': epoch}
torch.save(state, './model/model.pth')
# 加载模型
checkpoint = torch.load('./model/model.pth') # 加载断点
model.load_state_dict(checkpoint['model']) # 加载模型可学习参数
optimizer.load_state_dict(checkpoint['optimizer']) # 加载优化器参数
epoch = checkpoint['epoch'] # 设置开始的epoch数

模型的可视化

要对模型进行可视化，可以使用 torchsummary 库。这个库可以方便地打印出模型的结构和参数数量。

from torchsummary import summary

model = Model()
summary(model, (1, 28, 28)) # 输入数据的维度为 (batch_size, channels, height, width)

输出结果如下：

----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1           [-1, 64, 28, 28]             640
              ReLU-2           [-1, 64, 28, 28]               0
            Conv2d-3          [-1, 128, 28, 28]          73,856
              ReLU-4          [-1, 128, 28, 28]               0
         MaxPool2d-5          [-1, 128, 14, 14]               0
            Linear-6                 [-1, 1024]      25,691,136
              ReLU-7                 [-1, 1024]               0
           Dropout-8                 [-1, 1024]               0
            Linear-9                   [-1, 10]          10,250
================================================================
Total params: 25,775,882
Trainable params: 25,775,882
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 2.51
Params size (MB): 98.33
Estimated Total Size (MB): 100.84
----------------------------------------------------------------

还有一种可视化方法是使用 torchviz 库，这个库可以将模型的计算图可视化出来。这个需要下载Graphviz软件，然后将其添加到环境变量中,如 C:\Program Files (x86)\Graphviz2.38\bin。

# 模型的可视化
from torchviz import make_dot
x = Variable(torch.randn(1,1,28,28))
y = model(x)
g = make_dot(y)
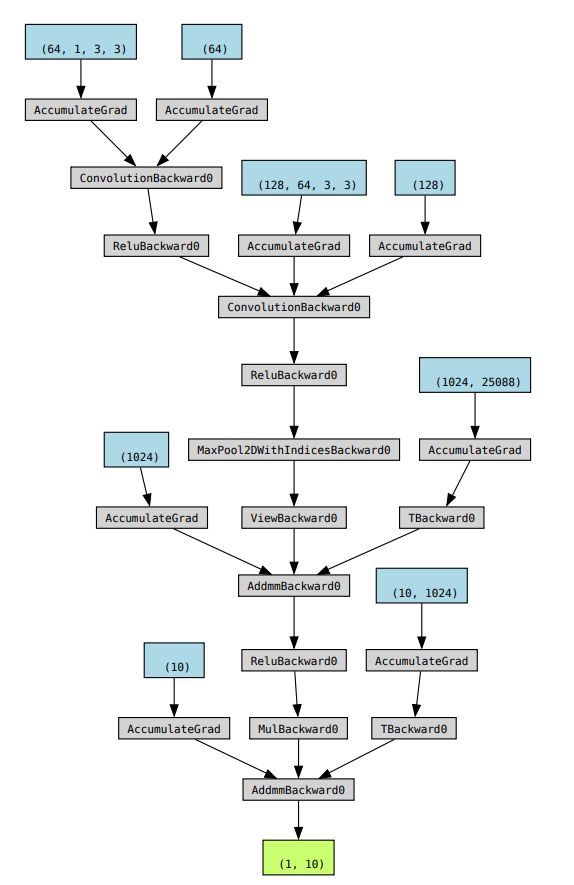
g.view()

输出结果如下：

20230527154944

nothing can stop me

陈同学

深度学习与图像处理（七）- Pytorch基础和手写数字识别实战

目录

机器学习工作流

Pytorch基础

GPU和CPU

张量Tensor

tensor中的运算

自动梯度

模型搭建和优化

torcn.nn

torch.optim

手写数字识别实战

数据增强data argumentation

数据预览和装载

模型搭建和参数优化

模型训练和优化

随机验证

保存模型

模型的可视化