神经网络的学习
神经网络的特征就是可以从数据中学习。所谓“从数据中学习”,是指可以由数据自动决定权重参数的值。
数据是机器学习的命根子。从数据中寻找答案、从数据中发现模式、根据数据讲故事……
训练集和测试集
机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和实验等。
首先,使用训练数据进行学习,寻找最优的参数;然后,使用测试数据评价训练得到的模型的实际能力。
为什么需要将数据分为训练数据和测试数据呢?因为我们追求的是模型的泛化能力。泛化能力是指处理未被观察过的数据(不包含在训练数据中的数据)的能力。获得泛化能力是机器学习的最终目标。
只对某个数据集过度拟合的状态称为过拟合(over fitting)。避免过拟合也是机器学习的一个重要课题。
mini-batch学习
如果遇到大数据,这种情况下以全部数据为对象计算损失函数是不现实的。因此,我们从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch, 小批量),然后对每个mini-batch 进行学习。
mini-batch: 从训练数据中随机选出一部分数据,这部分数据称为mini-batch。
损失函数
神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数(loss function)。这个损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
对该权重参数的损失函数求导,表示的是“如果稍微改变这个权重参数的值,损失函数的值会如何变化”。如果导数的值为负,通过使该权重参数向正方向改变,可以减小损失函数的值;反过来,如果导数的值为正,则通过使该权重参数向负方向改变,可以减小损失函数的值。不过,当导数的值为0 时,无论权重参数向哪个方向变化,损失函数的值都不会改变,此时该权重参数的更新会停在此处。
均方误差
mean squared error,MSE:
\[E = \frac{1}{2}\sum_{k}(y_k-t_k)^2\]这里,yk 是表示神经网络的输出,tk 表示监督数据,k 表示数据的维数。
交叉熵误差
cross entropy error,CEE:
\[E = -\sum_{k}t_k\log y_k\]这里,yk是神经网络的输出,tk是正确解标签。并且,tk中只有正确解标签的索引为1,其他均为0(one-hot 表示)。
梯度法
梯度法是一种求函数最小值的方法。梯度表示的是各点处的函数值减小最多的方向。梯度法是沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。这样一来,逐渐减小函数值的过程就是梯度法。
用梯度法寻找损失函数的最小值,寻找最优化参数(权重和偏置)。
用数学表达式来表示梯度法:
\[x _ { 0 } = x _ { 0 } - \eta \frac { \partial f } { \partial x _ { 0 } }\]在这个式子中,$\eta$表示学习率(Learning rate),这个需要事先设定,比如说0.01或者0.001。
神经网络的学习包括,(1)选取训练集和测试集;(2)梯度计算;(3)更新参数;(4)重复以上操作。
误差反向传播法
通过数值微分计算神经网络的权重参数的梯度计算量大,因此,我们使用误差反向传播法(error backpropagation)来高效地计算梯度。
计算图
计算图可以将计算过程用图形来表示,通过多个节点和边表示。如图所示,下面的计算图表示
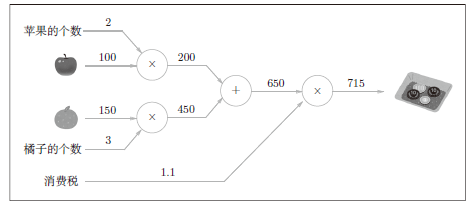
构建计算图,然后从左到右计算的过程叫做正向传播,从右往左的计算过程叫做反向传播。通过将数据正向和反向传播,可以高效地计算权重参数的梯度。
与学习有关的技巧
权重的初始值
在神经网络的学习中,权重的初始值特别重要。实际上,设定什么样的 权重初始值,经常关系到神经网络的学习能否成功。
一般会将初始值设为较小的值。比如说,权重初始值设置成0.01 * np.random.randn(10, 100)这样,使用由高斯分布生成的值乘以0.01 后得到的值(标准差为0.01 的高斯分布)。
权重的更新
SGD 随机梯度下降
随机梯度下降的思想就是随机采样一个样本来更新参数,SGD每次迭代仅对一个样本计算梯度,直到收敛。
SGD的缺点是,如果函数的形状非均向(anisotropic),比如呈延伸状,搜索 的路径就会非常低效。因此,我们需要比单纯朝梯度方向前进的SGD更聪明的方法。SGD低效的根本原因是,梯度的方向并没有指向最小值的方向。
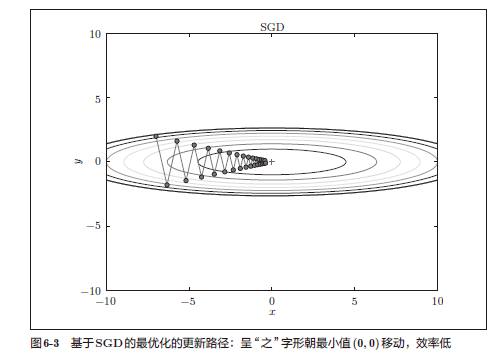
Momentum
\[v \leftarrow \alpha v- \eta \frac{\partial L}{\partial W} \\ W+W+v \\\]这里新出现了一个变量v,对应物理上的速度。表示了物体在梯度方向上受力,在这个力的作用下,物体的速度增加这一物理法则。
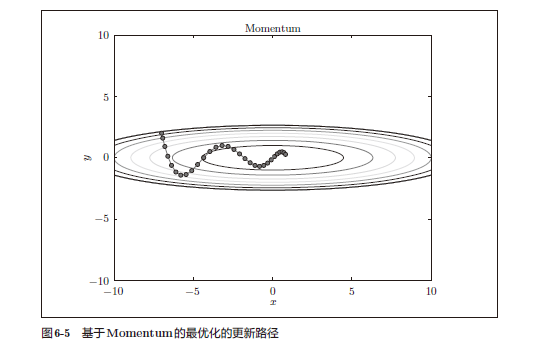
AdaGrad
AdaGrad会为参数的每个元素适当地调整学习率,与此同时进行学习。
\[h \leftarrow h+ \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W}\] \[W \leftarrow W- \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W}\]这里,W表示要更新的权重,$\frac{\partial L}{\partial W}$表示损失函数关于W的梯度,$\eta$表示学习率,h表示一个变量,初期时所有元素都为0,它保存了以前的所有梯度的平方和,$\odot$表示矩阵的按元素乘法。
因此,AdaGrad会使得学习率逐渐减小(学习率衰减)。
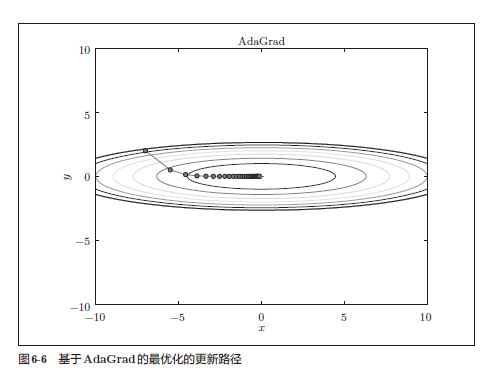
Batch Normalization
Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。
Batch Norm有以下优点。
- 可以使学习快速进行(可以增大学习率)。
- 不那么依赖初始值(对于初始值不用那么神经质)。
- 抑制过拟合(降低Dropout等的必要性)。
正则化
过拟合
发生过拟合主要有以下两个原因:
- 模型拥有大量参数、表现力强
- 训练数据少
权重衰减
权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过 在学习的过程中对大的权重进行惩罚,来抑制过拟合。
Dropout 是一种在学习的过程中随机删除神经元的方法。训练时,随机 选出隐藏层的神经元,然后将其删除。被删除的神经元不再进行信号的传递。
超参数的验证
除了权重和偏置等参数,超参数(hyper-parameter)也经常出现。这里所说的超参数是指,比如各层的神经元数量、batch 大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值,模型的性能就会很差。
不能使用测试数据评估超参数的性能。
为什么不能用测试数据评估超参数的性能呢?这是因为如果使用测试数 据调整超参数,超参数的值会对测试数据发生过拟合。可能就会得到不能拟合其他数据、泛化能力低的模型。
因此,调整超参数时,必须使用超参数专用的确认数据。用于调整超参数的数据,一般称为验证数据(validation data)。我们使用这个验证数据来评估超参数的好坏。
(x_train,t_train),(x_test,t_test)=load_mnist()
# shuttle the data
x_train,t_train = shuffle_data(x_train,t_train)
# seperate validation data
validation_rate = 0.20
validation_num = int(x_train.shape[0]*validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
集成学习
让多个模型进行学习,推理时再取多个模型的输出的平均值。





