深层神经网络
与浅层神经网络相比,深层神经网络的层数更多,参数更多,计算量更大,但是可以更好地拟合数据,提高模型的准确率。

我们思考一个问题,每次输出数据的各个节点是从输入数据的哪个区域计算得到的呢?下图是重复两次3×3的卷积计算的情形,可以看到,输出数据的各个节点都来自于输入数据的一个5×5的区域,这个区域称为感受野。
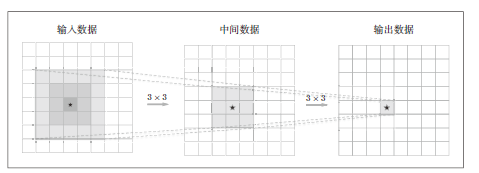
也就是说,一次5 × 5 的卷积运算的区域可以由两次3 × 3 的卷积运算抵充。并且,相对于前者的参数数量25(5 × 5),后者一共是18(2 × 3 × 3),通过叠加卷积层,参数数量减少了。同时,可以扩大感受野(receptive field)。通过叠加层,在卷积层中间加入ReLU层,可以叠加非线性,提高模型的表达能力。
经典的深度网络
VGG
VGG是由卷积层和池化层构成的基础的CNN,它的特点在于将有权重的层(卷积层或者全连接层)叠加至16 层(或者19 层),具备了深度(根据层的深度,有时也称为“VGG16”或“VGG19”)。
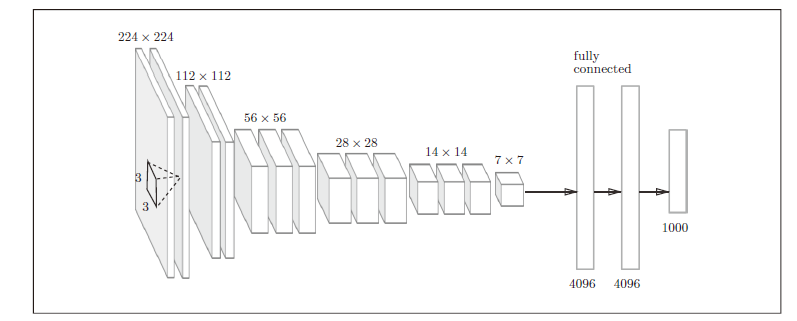
VGG中需要注意的地方是,基于3×3 的小型滤波器的卷积层的运算是连续进行的。如图所示,重复进行“卷积层重叠2 次到4 次,再通过池化层将大小减半”的处理,最后经由全连接层输出结果。
GoogLeNet
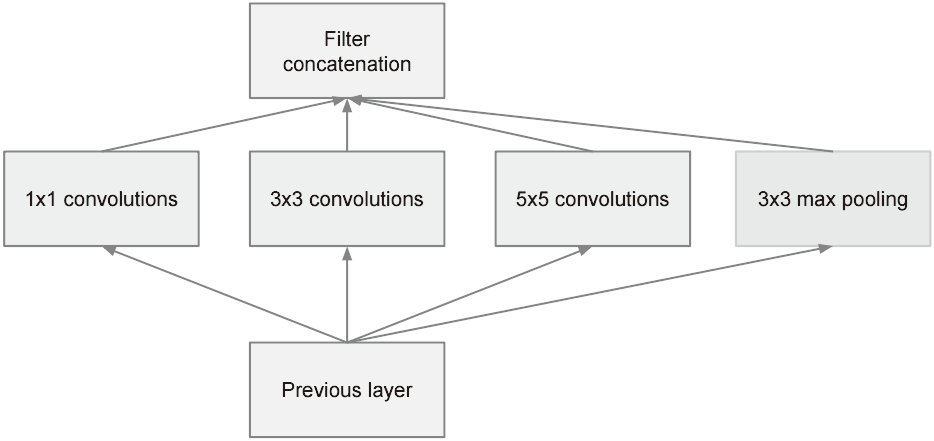
GoogLeNet的特征是,网络不仅在纵向上有深度,在横向上也有深度(广度),这称为“Inception 结构”。
如图所示,Inception 结构使用了多个大小不同的滤波器(和池化),最后再合并它们的结果。GoogLeNet 的特征就是将这个Inception 结构用作一个构件(构成元素)。此外,Inception中大量采用了1×1的卷积运算,这是因为1×1的卷积运算可以用来控制通道数,从而控制数据的维度。
ResNet
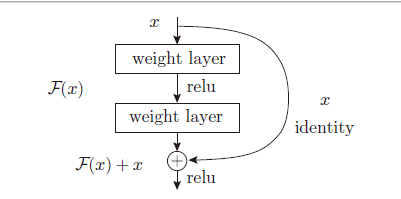
快捷结构将数据原封不动地传向下游。因此,基于快捷结构,不用担心梯度会变小(或变大),之前因为加深层而导致的梯度变小的梯度消失问题就有望得到缓解。
迁移学习
实践中经常会灵活应用使用ImageNet 这个巨大的数据集学习到的权重数据,这称为迁移学习,将学习完的权重(的一部分)复制到其他神经网络,进行再学习(fine tuning)。比如,准备一个和VGG 相同结构的网络,把学习完的权重作为初始值,以新数据集为对象,进行再学习。迁移学习在手头数据集较少时非常有效。





