循环神经网络简介
循环神经网络(Recurrent Neural Network, RNN)
循环神经网络的主要用途是处理和预测序列数据,传统的神经网络模型中,我们假设所有的输入都是相互独立的,从输入层到隐藏层再到输出层,层与层之间是全连接的,每层之间的节点是无连接的。但是在实际生活中,很多数据都是有前后关系的,比如自然语言,我们在看一段话的时候,往往是要根据前面的话才能理解后面的话的。循环神经网络就是为了解决这种时序相关性的问题而提出的。
RNN隐藏层相互连接,也即是一个序列的输出与前面的输出也有关,也拥有捕获已计算节点信息的记忆能力。RNN的隐藏层可以看成是一个内部的循环,信息可以在这个循环中传递,这也是RNN名字的由来。
循环神经网络展开如下:
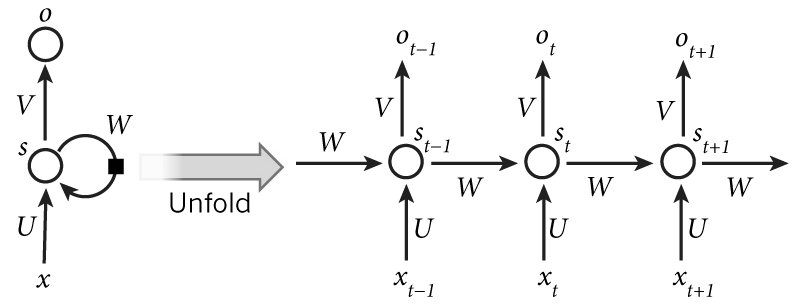
其中,x 是输入层的值,s 是隐藏层的值,U 是输入层到隐藏层的权重矩阵。 o 表示输出层的值,V 是隐藏层到输出层的权重矩阵。循环神经网络的隐藏 层的值s 不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵W 就是隐藏层上一次的值作为这一次的输入的权重。RNN 每一层的权重 W 都是共享的。总体 Loss 由每一步的 Loss 组合而成。
在这张图片中,$x_t$表示t=1,2,…,T时刻的输入,$s_t$是隐藏层第t步的状态,由当前步骤的输入和先前隐藏状态共同计算得到求得:
\[S_t = f(Ux_t + Ws_{t-1})\]$O_t$是t时刻的输出。
循环神经网络中由于输入时叠加了之前的信号,所以反向传导时不同于传统的神经网络,需要对每个时间步的参数进行更新,这就是所谓的BPTT算法(Back Propagation Through Time-BPTT)。
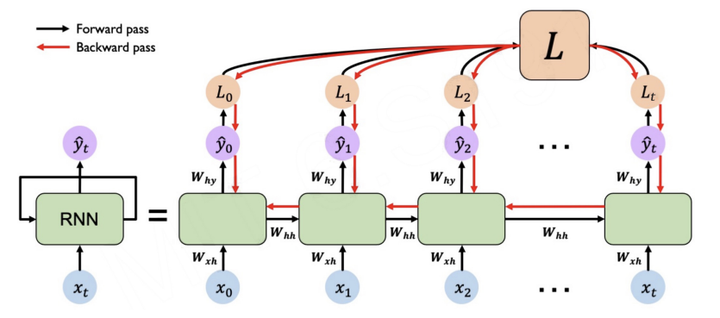
前向传播过程中:
\[\begin{array}{ll} s_1=f\left(U x_1+W s_0+b\right) & o_1=g(V s_1+c) \\ s_2=f\left(U x_2+W s_1+b\right) & o_2=g(V s_2+c) \\ s_3=f\left(U x_3+W s_2+b\right) & o_3=g(V s_3+c) \end{array}\]反向传播过程中,对于每个时间步,都需要计算相应的梯度,然后将梯度进行累加,最后对参数进行更新。
我们这里计算t=3时刻的U、V、W的求损失函数L_3的偏导:
\[\begin{aligned} \frac{\partial L_3}{\partial U} & =\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial U}+\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \frac{\partial S_2}{\partial U}+\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \frac{\partial S_2}{\partial S_1} \frac{\partial S_1}{\partial U} \\ \frac{\partial L_3}{\partial V} & =\frac{\partial L_3}{\partial S_3} \frac{\partial S_3}{\partial V} \\ \frac{\partial L_3}{\partial W} & =\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial W}+\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \frac{\partial S_2}{\partial W}+\frac{\partial L_3}{\partial O_3} \frac{\partial O_3}{\partial S_3} \frac{\partial S_3}{\partial S_2} \frac{\partial S_2}{\partial S_1} \frac{\partial S_1}{\partial W} \end{aligned}\]若t足够大,则式子中的加数就很多,任意时刻t时对U、W求偏导,以W为例:
\[\frac{\partial L_t}{\partial W}=\sum_{k=0}^t \frac{\partial L_t}{\partial O_t} \frac{\partial O_t}{\partial S_t}\left(\prod_{j=k+1}^t \frac{\partial S_j}{\partial S_{j-1}}\right) \frac{\partial S_j}{\partial W}\]可以看出,当时间序列足够长,t足够大时,梯度会指数级的衰减,这就是著名的梯度消失问题,伴随着梯度消失的是RNN的记忆能力的衰减,这使得RNN难以捕捉到时间序列中时间跨度较大的依赖关系。
LSTM网络的出现就是为了解决这个问题。
GRU
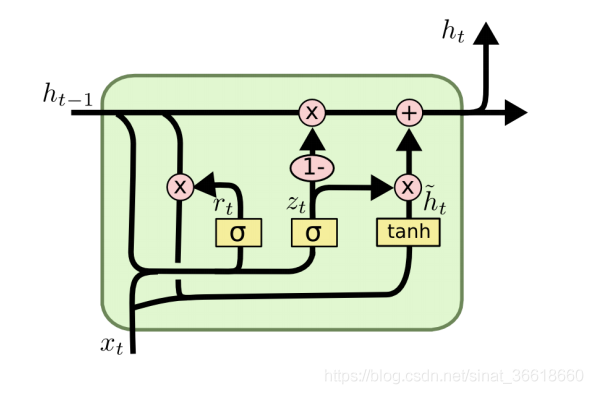
GRU是LSTM的变体,它将LSTM中的输入门和遗忘门合并成了一个更新门,同时合并了细胞状态和隐藏状态,使得模型更加简单。每个前面状态对当前的影响都进行了距离加权,距离越远,权重越小。
GRU网络结构如下:
参考文献:





