1. 风电场数据基本特点
由于机械故障、天气因素和人为影响等原因,风场内风速数据出现采集时间短、间断点多、数据失真等诸多问题,给风资源的评估带来不小的麻烦。
1.1 风电场数据基本类型
风电场内的数据根据数据来源情况可分为两类:一类是风电机组运行数据,即SCADA机组数据;另一类是风资源测量数据,主要是测风塔测量数据,测风塔测量成本低,可靠性高,在风电场前期规划与后期运行过程中占据地位。多普勒激光雷法也可以测量风速,但因为成本过高在风电场中一些高精度研究项目才会使用。1
1.1.1 SCADA数据
SCADA数据记录了风电机组运行期间的各种详细数据,包括风向、风速、温度等环境参数,以及输出功率、电流、电压等机组功率参数,桨距角。偏航等发电控制策略参数以及各种转速等运行监测数据。1 其中,比较重要的是机舱风速和输出功率。
1.1.2 测风塔数据
是当地风资源的主要数据来源,包括当地长期的风速、风向、温度等环境参数。测风塔数据的采集周期一般为10min,数据采集不止一个高度,数据量较大。1
1.1.3 激光雷达测风数据
激光雷达的测量以激光脉冲多普勒频移原理为基础,是一种测量精度高但是成本高的测风方式,可以测得几十米到几百米范围内多层高的风速、风向、温度等数据,采样频率高,数据层数多,但是由于成本较高,一般得到的都是几个月长度的短期数据。1
1.1.4 其他数据
其他气象数据还包括气象站点数据、卫星数据、模型数据以及再分析数据集。
其中,再分析数据集如CFSR,ERA-5,ERA-Interim, MERRA-2, NCEP/NCAR Reanalysis I等数据集,是一种基于数值模式并且同化融合了实测数据的再分析数据集,其数据时间跨度长,空间分辨率高,数据质量高,是风资源评估中常用的数据来源。
1.2 风电场数据缺失情况
1.2.1 机组运行数据缺少情况
从缺失数据分布来看,主要存在以下几种情况:
- 离散缺失:在某些时刻数据出现缺失情况,缺失位置的前后时间与同时刻机组数据正常;
- 少量缺失:少量机组同时出现数据缺少的情况,通常是由于通信问题造成的;
- 严重缺失:同一时间大量机组数据缺少,通常是由于机组停机造成的。
考虑到风电场内不同机组的风速具有较大的相关性,当运行风速数据出现离散缺失和少量缺失的情况下,可以使用其他机组的风速对缺失数据进行插补和重构。
1.2.2 风电场数据缺失原因
1.3 除了数据缺失之外其他需要插补的原因
除了测量仪器故障之外,在工程设计时,有部分项目由于工程进度要求,在未收集到一个完整年测风数据的情况下就需完成对风电场风能资源及发电量的评估,为保障评估结果的合理性,也要对不满一年的测风数据进行插补订正。2
同时,根据《风电场工程风能资源测量与评估技术规范》(NB/T 31147-2018),测风塔所选时间段的有效数据完整率应达到90%以上,测风时长满足连续一个完整年,因此对于缺测或者无效的数据需要采取插补的方法以提高数据完整率和测风时长。3
2. 数据插补方法
2.1 传统风速插补方法
现阶段风电行业内采用基于相关测量预测方法(MCP,Measure-Correlate Predict)(可称之为传统插补方法)进行间断数据的插补和拟合。
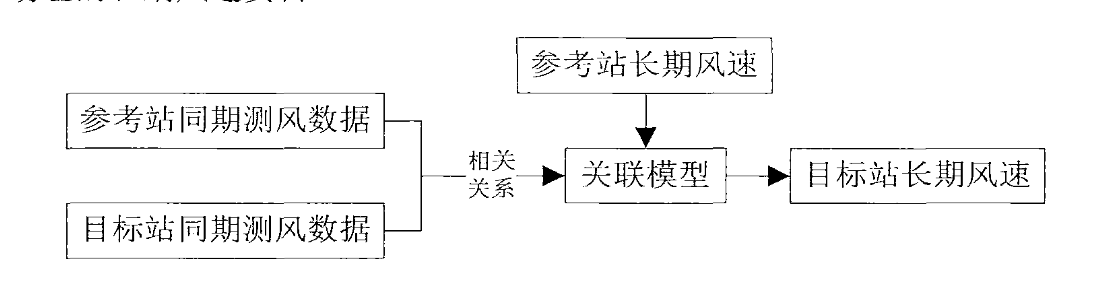
传统的插补方法包括测量相关预测方法(Measure-correlate-predict,MCP)4,它主要是利用目标站点短期测风数据(风速、风向)以及长期参考数据预测目标站点长期风况。该方法可以利用参考数据修正测风期间由于仪器受损、人为因素等原因造成的数据缺失。
目标站点一般是测风塔的测风数据,参考数据选择目标站点附近与其地形相似且气候条件相近、风能资源分布相似、长时间(10年以上的)实测气象数据和再分析数据。
有如下八种MCP算法:线性回归法、正交回归法、矩阵时间序列法、快速排序法、方差比法、风速比法、垂直分层算法以及 威布尔拟合算法。
也就是说,MCP算法第一步就是建立参考站点和目标站点的关联模型,其中,线性回归法和方差比法是最常用的两种方法。
2.1.1 线性回归法
也叫作线性最小二乘法(LLS),LLS算法的拟合曲线是一条拟合曲线:
\[\left\{\begin{array}{c} y=m x+b \\ m=S_{x y} / S_{x x} \\ b=\bar y-m \bar x \\ S_{x y}=\sum_{i=1}^{n} (x_{i} - \bar x)(y_{i} - \bar y) \\ S_{x x}=\sum_{i=1}^{n} (x_{i} - \bar x)^{2} \end{array}\right.\]y代表线性回归得到的目标站风速,x代表参考站风速,m和b分别代表线性回归的斜率和截距,$S_{x y}$和$S_{x x}$分别代表参考站风速和目标站风速的协方差和方差。
2.1.2 方差比法
采用线性回归的方法时,得到的目标站风速的预测值和实际值之间比较接近,但是预测值的方差会远远小于观测得到目标站的方差,这导致了风速分布的不准确。为了解决这个问题,方差比法被提出。
其他统计方法
2.2.2 三次样条插值法
缺点:自然风速时间序列是一个波动强烈的非线性时间序列,Lagrange、三次样条和线性插值等传统插值算法中,任意两个信息点之间用直线或者光滑的曲线连接,掩盖了相邻插值点间的局部变化特征,因此用于波动强烈的风速时间序列效果并不理想(用于频率相对稳定的低频和中频曲线插值效果比较理想)。6
2.3 物理模型插补方法
物理模型通过发现、归纳和求解规律的方式实现风速的预测。如大气运动基本方程组,可以通过求解方程组得到风速的预测值。
气象特征包括风向、温度、相对湿度、露点温度、气压和海平面气压。这些 因素与风速的时序变化存在复杂的非线性相关性的因素。因此,气象特征的预测是风速预测的重要组成部分。
\[\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} = - \frac{1}{\rho} \frac{\partial p}{\partial x} + f v + \nu \nabla^2 u\] \[\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} = - \frac{1}{\rho} \frac{\partial p}{\partial y} - f u + \nu \nabla^2 v\] \[\frac{\partial p}{\partial z} = - \rho g\] \[\frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} + w \frac{\partial T}{\partial z} = \frac{1}{\rho c_p} \left( \frac{\partial q}{\partial x} + \frac{\partial q}{\partial y} + \frac{\partial q}{\partial z} \right) + \nu \nabla^2 T\] \[p = \rho R T\]2.4 分形维数插补方法
分形理论作为非线性科学中的一个分支,可以定性或定量分析不规则的几何 体和复杂现象。钟莉等从全国80个典型站点风速记录的关联维数统计得知,风速时程的分形维数均约在1.7左右。7 利用分形的理论和分析方法对测风场的时间序列进行描述和研究,可以更好地揭示风场的内在规律,从而为风电场的设计和运行提供理论依据。8
2.5 机器学习插补方法
机器学习的主要任务之一是分类问题,它的目标是将输入数据分成不同的类别。分类问题通常用于识别图像、语音、文本等数据类型。另一个主要任务是回归问题,它的目标是预测一个连续的输出变量。回归问题通常用于预测房价、股票价格、销售量等连续变量。因此,使用机器学习进行数据插补属于回归问题。
2.5.1 KNN
一种基本的分类方法是 k 最近邻 (kNN) 算法。类成员是 k-NN 分类的结果。
项目的分类取决于它与训练集中的点的相似程度,该对象将进入其 k 个最近邻中成员最多的类。如果 k = 1,则该项目被简单地分配给该项目最近邻居的类。使用缺失数据找到与观测值最近的 k 邻域,然后根据邻域中的非缺失值对它们进行插补可能有助于生成关于缺失值的预测。
2.4.2 随机森林
随机森林
2.5.3 支持向量回归
2.6 时间序列模型插补法
常用的平稳时间序列模型主要包括:自回归模型(AR模型)、移动平均模型(MA)和自回归移动平均模型(ARMA)。建立AR,MA,ARMA,ARIMA模型,对风速进行预测,然后将预测值填充到缺失值中。
2.7 多重插补法
多重插补(Mutiple imputation,MI)的思想来源于贝叶斯估计,认为待插补的值是随机的,它的值来自于已观测到的值。具体实践上通常是估计出待插补的值,然后再加上不同的噪声,形成多组可选插补值。根据某种选择依据,选取最合适的插补值。
多重插补法大致分为三步:
为每个空值产生一套可能的插补值,这些值反映了模型的不确定性;每个值都被用来插补数据集中的缺失值,产生若干个完整数据集合。 每个插补数据集合都用针对完整数据集的统计方法进行统计分析。 对来自各个插补数据集的结果进行整合,产生最终的统计推断,这一推断考虑到了由于数据插补而产生的不确定性。该方法将空缺值视为随机样本,这样计算出来的统计推断可能受到空缺值的不确定性的影响。
2.7.1 MICE简介
通过链式方程进行的多元插补(MICE,Multiple Imputation by Chained Equations),与单个插补(例如均值)相比,创建多个插补可解决缺失值的不确定性。MICE假定缺失的数据是随机(MAR)的,这意味着,一个值丢失概率上观测值仅取决于并且可以使用它们来预测。通过为每个变量指定插补模型,可以按变量插补数据。
2.8 深度学习插补方法
2.5.1 DNN
2.5.2 CNN
2.5.3 GRU
2.5.4 LSTM
2.5.5 MLP
2.5.6 VAE
变分自编码器(Variational Auto-Encoders,VAE)作为深度生成模型的一种形式,是由 Kingma 等人于 2014 年提出的基于变分贝叶斯(Variational Bayes,VB)推断的生成式网络结构。与传统的自编码器通过数值的方式描述潜在空间不同,它以概率的方式描述对潜在空间的观察,在数据生成方面表现出了巨大的应用价值。
工作思路如下:
比如说。利用最邻近机组风速,选取两台风速相关性最大的得到一个两列的风速序列,并且每行数据对应时间相同:将这两列数数据划分为训练集与测试集,以训练集中第一台机组风速作为输入,第二台机组风速作为输出对模型进行训练;模型训练完成后,将测试集中第一台机组风速输入模型,输出第二台机组风速的重构序列,重构序列与测试集中第二台机组风速具有相同的数据特征:对测试集中第二台机组风速序列进行污染,使用重构序列对应位置数据对污染后的序列进行填充,达到数据插补的目的。主要是是利用同一风场不同机组间风速的空间相关性,这主要是应对离散缺失和少量缺失的情况。1
对于数据缺失比较严重的情况,可以考虑使用LSTM神经网络对风速序列进行重构:基本工作思路如下,首先得到一个风速数据的时间序列,在序列中添加噪声获得大段时间缺失后的风速序列,使用LSTM对风速序列进行重构,得到一组新的风速序列,该序列与原始数据具有相同的数据特征,可以评估插补效果。1
3. 插补方法的评价指标
为了衡量数据插补的效果,分析插补后的数据和真实值之间的偏差,需要定义一些评价指标。
3.1 插补方法的评价指标
偏差 Bias:
\[Bias = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)\]平均绝对误差 mean absolute error (MAE):
\[MAE = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|\]范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
均方误差 mean squared error (MSE):
\[MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2\]范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
均方根误差 root mean squared error (RMSE):
\[RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i - \hat y_i)^2}\]范围[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;误差越大,该值越大。
纳什效率系数 Nash-Sutcliffe efficiency (NSE):
\[NSE = 1 - \frac{\sum_{i=1}^n (y_i - \hat y_i)^2}{\sum_{i=1}^n (y_i - \bar y)^2}\]其中,$\hat y_i$为预测值,$y_i$为真实值,n为样本数,$\bar y$为真实值的均值。
4. 结论与展望
- 风电场测风数据主要包括测风塔数据和激光雷达数据,测风塔数据完整性较好,激光雷达数据测量精度高,测量高度范围打,但是存在测量时间短和高层数据缺失量大的问题。
- 不同地形风电场都存在数据缺失的情况,内陆平坦地形风电场主要是少量缺失与严重缺失情况;复杂山地地形风电场同时存在离散缺失和严重缺失情况。